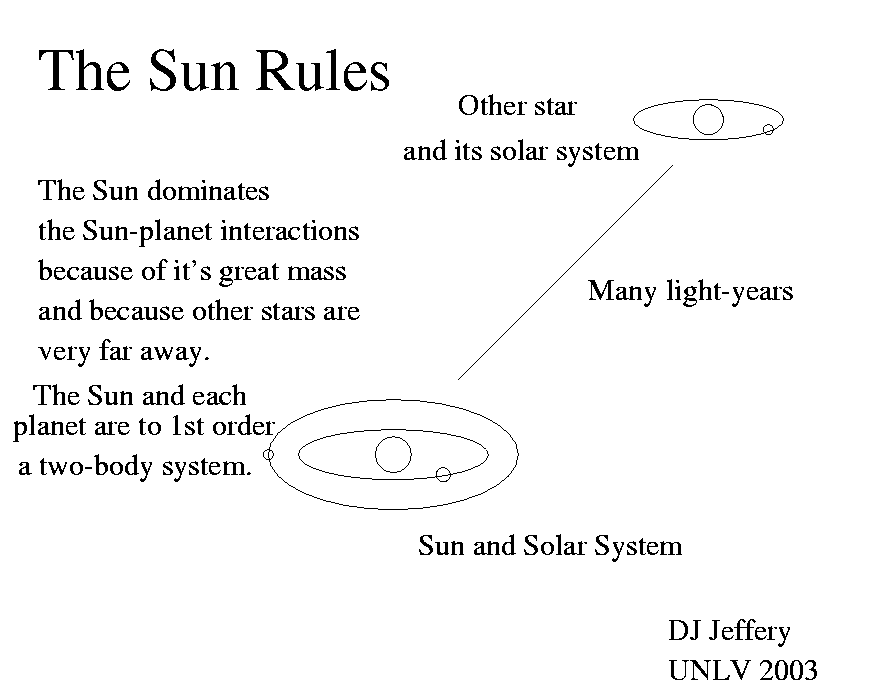
Caption: The Solar-System and a general remote planetary system.

Features:

1. Newtonian physics shows that two gravitationally bound spherically-symmetric astro-bodies absolutely isolated will orbit their mutual center of mass in exact elliptical orbits with the center of mass at focus of each of the elliptical orbits---the other focuses are just empty points in space---as is the center of mass itself if it is NOT actually in one of the astro-bodies. If the mass of one astro-body is overwhelmingly dominant, that astro-body's center becomes effectively the center of mass that the other astro-body orbits in an elliptical orbit.

2. There is, in fact, an exact analytic solution (i.e., a formula) for the gravitational two-body system just described above. There are, in fact, no other gravitationally bound systems with an exact solution in general although there are special case solutions (see Wikipedia: Three-body problem; three_body_system.html). All gravitationally bound systems beyond with more than 2 astro-bodies must treated (except for the aforementioned special cases) by perturbation theory or by numerical solution ground out by the computer.

3. But you say, gravitational two-body systems (as described) do NOT actually exist, and so how can the exact solution be useful.

   The exact gravitational two-body system is an ideal limit that is actually approached very often in the astrophysical realm, and so the exact solution is often an excellent approximation to 1st order or a good starting point for perturbation theory.

4. Let's expand a bit on the foregoing by considering the internal interactions of a localized multi-body gravitationally bound system with a overwhelmingly dominant body by mass: e.g., a planetary system with a dominant star (like the Solar System) or a moon system with a dominant planet (like Jupiter moon system).

   In such a gravitationally bound system, the gravitational interaction between the dominant body and each other body individually is approximately a gravitational two-body system to 1st order. The other bodies cause gravitational perturbations and those have to be accounted for to 2nd order in detailed analyses often by perturbation theory or you find a accuracy/precision numerical solution using the computer.

5. But what of the all the enormous massive bodies throughout the observable universe? They must have an effect on the localized multi-body gravitationally bound system.

   Yes. Gravity in the classical limit is an inverse-square law force. Now in one sense, inverse-square law forces fall off rapidly with distance: e.g., double distance and the force decreases by a factor of 4. However, in another and important sense they are long-range forces since formally they do NOT go to zero until you reach infinity. So Newtonian physics predicts all the enormous massive bodies throughout the observable universe do have an effect on the localized multi-body gravitationally bound system. General relativity (the more adequate theory) gives the same result.

   However, Newtonian physics (with some extra hypotheses) and general relativity (without extra hypotheses) tells us that if the bodies outside of the localized multi-body gravitationally bound system are sufficiently far off relative to size scale of the gravitationally bound system, then they create a sufficiently uniform gravitational field that internal motions of the localized multi-body gravitationally bound system relative to its center of mass are determined only by internal forces. The external forces only determine the trajectory of the center of mass of the localized multi-body gravitationally bound system. This situation often holds: e.g., for example for most planetary systems (like the Solar System) and most moon systems (like the Jupiter moon system).

   The upshot is that the exact solution from Newtonian physics for the gravitational two-body system is verified again as a useful approximation provided the multi-body gravitationally bound system has a single dominant source of gravity: e.g., a dominant star in a planetary system and a dominant planet in a moon system.