Image 1 Caption: An animation of a gravitationally-bound three-body system showing the approximate orbital trajectories of three identical point masses initially at rest in the inertial frame defined by their mutual center of mass. The point masses are, of course, located at the vertices a triangle which at almost all times is a scalene triangle. The center of mass stays at rest in obedience to the law of conservation of momentum.

Features:

1. The three-body system in the animation is probably NOT in a periodic solution (of the three-body problem), but the original caption of the animation made NO definite statement. The solution, in fact, is probably chaotic. The solution was probably calculated by an N-body simulation.

   

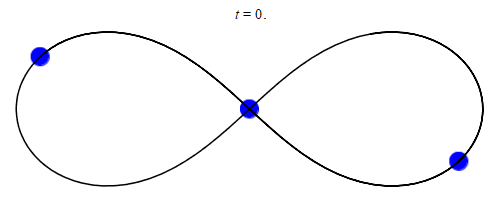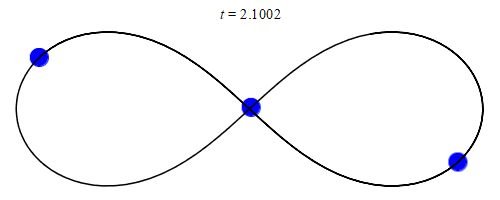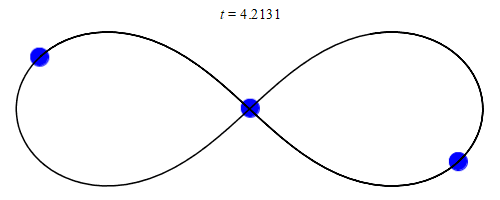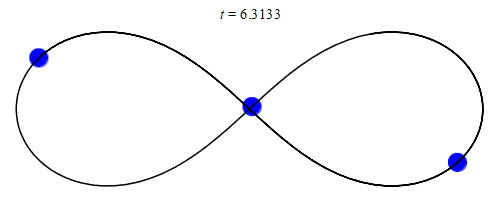
2. Image 2 Caption: An animation of the figure-8 orbit solution for a gravitationally bound three-body system over a single orbital period of T = 6.3259 in some time unit (see Wikipedia: Three-body problem: Special-case solutions).

3. The solution in this case is periodic. Thus, it is an exact periodic solution of the three-body system. However, there is NO closed-form formula (i.e., NO formula one can just write down). The figure-8 orbit solution is (neutrally) stable to small astronomical perturbations, but its range of (neutral) stability is very small. So it probably occurs only rarely and fleetingly in nature and has NEVER been observed.

4. Note stability for orbits is usually neutral stability in yours truly's understanding. So astronomical perturbations cause changes that are NOT damped out as for stable equilibriums, but the changes do NOT grow without bound as for unstable equilibriums. The changes are in a vague sense stay roughly proportional to the astronomical perturbations. However, stable equilibriums and unstable equilibriums do occur for orbits. For example, consider the Lagrange point orbits. The L4 and L5 points are stable equilibriums and the L1, L2, and L3 points are unstable equilibriums. For more on the Lagrange points, see File lagrange_points.html.

5. See also the definition of figure eight (AKA figure 8).

1. Credit/Permission: © User:Dnttllthmmnm, 2017 / CC BY-SA 4.0.
   Image link: Wikimedia Commons: File:Three-body Problem Animation with COM.gif.
   
2. Credit/Permission: © User:MaxwellMolecule, 2019 / CC BY-SA 4.0.
   Image link: Wikimedia Commons: File:Three body problem figure-8 orbit animation.gif.