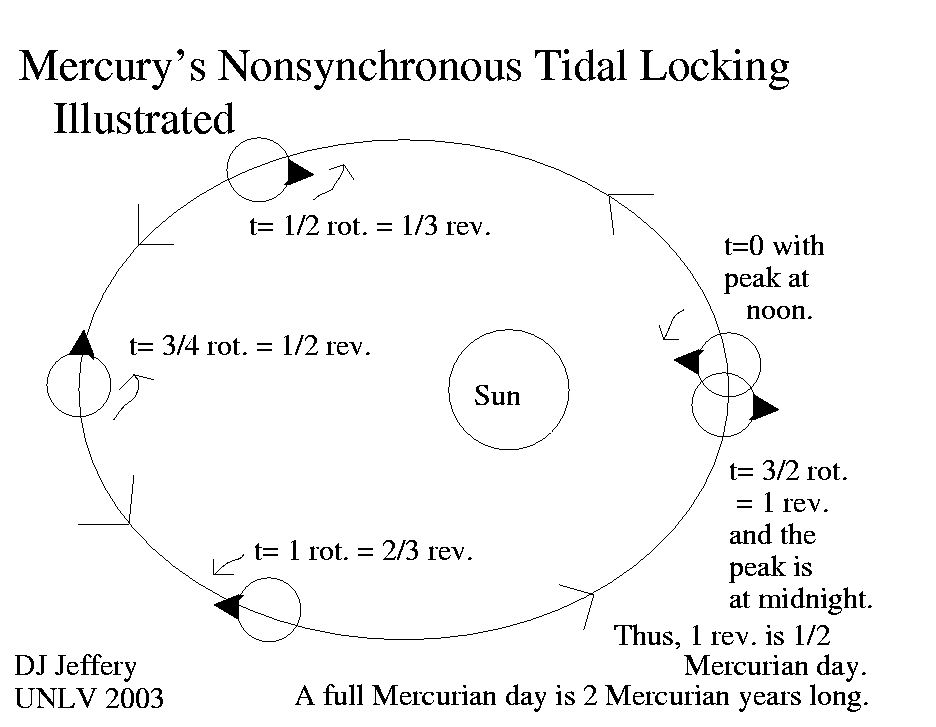
Caption: Mercury's orbit exhibits a 3:2 spin-orbit resonance which is illustrated in the diagram.

Features:

1. The relevant periods and relationships among them:
   1. orbital period (relative to the observable universe): Mercurian orbital rotation period P_O = 87.9691 days = 0.240846 yr = (3/2)*P_A = (1/2)*P_D.
   2. axial rotational period (relative to the observable universe): Mercurian axial rotational period P_A= 58.646 days = (2/3)*P_O = (1/3)*P_D.
   3. synodic day (i.e., rotation period relative to host star): Mercurian synodic day P_D = 175.942 days = 2*P_O = 3*P_A (NASA: Mercury fact sheet, 2021).
   The whole number ratios specified for the above periods are for the ideal 3:2 spin-orbit resonance. Astronomical perturbations cause the actual ratios to NOT be exactly whole number ratios, but they are very close to being that. In any case, observational uncertainty would prevent ever observationally determining exact whole number ratios even if they really were present.

2. By following the progress of the artificial giant mountain in the diagram, one can see clearly how the 3 relevant periods relate to each other.

3. To explicate one detail of the diagram:

   Say you land on Mercury on the equator just at noon on top of a giant mountain.

   Now 3/2 axial rotation periods later, 1 Mercurian year has passed (i.e., Mercurian orbital rotation period P_O = 87.9691 days = 0.240846 yr = (3/2)*P_A = (1/2)*P_D has passed).

   But since it is 3/2 axial rotation periods, it is now midnight for you.

   It takes another 3/2 axial rotation periods to bring you back to noon.

   Thus the Mercurian synodic day P_D = 175.942 days = 2*P_O = 3*P_A (i.e., noon to noon) is 3 axial rotation periods = 2 orbital periods (i.e., 2 Mercurian years).

4. In the case of Mercury, the large eccentricity of the Mercurian orbit (e=0.0.205630 ≅ 20 %) caused it to settle into a stable 3:2 spin-orbit resonance and this is according to one theory happened within 20 Myr of Mercury's formation (Wikipedia: Mercury: Spin-orbit resonance).

   Subtle stabilizing effects damp out any changes in the ratios set by the 3:2 spin-orbit resonance caused by astronomical perturbations.

5. A resonance is tendency for large and/or stable oscillations.

   In the case of Mercury's orbit, the oscillations are axial rotations and orbit rotations.

6. The 3:2 spin-orbit resonance situation gives 3 rotation periods = 3 * 58.646 days ≅ 175.942 days nearly exactly equal to the time of 2 orbital periods 2 * 87.9691 days ≅ 175.942 days (see Wikipedia: Mercury; Wikipedia: Mercury: Spin-orbit resonance; NASA: Mercury fact sheet, 2021).

   From the specialized formulae for the synodic period (see Orbit file: synodic_period.html), we have, in fact, Mercurian day equal to 2 orbital periods = 175.9382 days. The diagram also shows why this must be so (as aforesaid).

   The accurate Mercurian day = 175.942 days (NASA: Mercury fact sheet, 2021). The discrepancy between our calculated value and NASA's may be due to the specialized formulae being based on assumption that Mercury having a circular orbit which is NOT the case. There might be other reasons for the slight discrepancy: e.g., astronomical perturbations and/or observational error.

7. Before Doppler radar observations in 1965, people thought Mercury would be tidally locked to the Sun (see Wikipedia: Mercury: Spin-orbit resonance).

8. Old scifi novels and short stories (pre-1965) often make a point of the supposed tidal locking of Mercury and sometimes give Mercury a habitable zone at its fixed terminator (the line between daytime and nighttime).