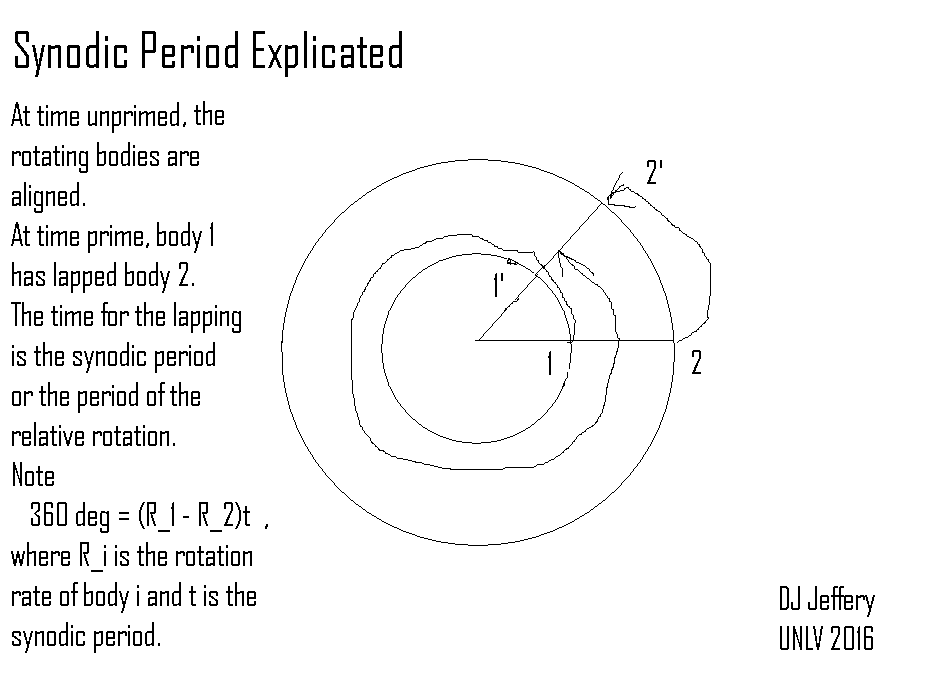
Caption: An explication of synodic period.

Features:

A synodic period is a period of a rotation (either orbital revolution or axial rotation about a fixed axis) relative to another rotation.
For variant definition of synodic period that amounts to much the same thing, see Wikipedia: Orbital period.
For example, the period between oppositions/conjunctions (as seen from Earth) is the synodic period for a planet since it is the rotation period of the planet's orbital revolution relative to the Earth's orbital rotation.
The term synodic period is usually NOT used for rotations relative to inertial frames and when NOT, the rotation can be classified a geometrical rotation rather than a physical rotation since that is relative to an inertial frame.
As examples of synodic periods, see the animation in the figure below (local link / general link: prograde_retrograde.html). Each moon in the animation has a set of synodic periods for its rotations relative to the other moons and the planet's axial rotation.
Synodic periods are important because they are often direct observables when physical rotation periods are NOT direct observables. This importance was particularly important in astronomy history in establishing the orbital periods of the planets.
One needs formulae to convert back and forth between synodic periods and basic rotation periods (e.g., those relative to inertial frames).
Below, we derive the needed formulae for a useful simplified special case: i.e., the specialized formulae for the synodic period.
Derivation:
1. We make the simplyfing assumption that all the basic rotations are uniform circular motions in a common plane. This assumption can be dispensed with, but that leads one to formulae that are too complex for educational purposes.
2. For definiteness, we consider counterclockwise/clockwise rotations as prograde/retrograde rotations. The prograde/retrograde rotations have positive/negative rotation rates and rotation periods.
3. Consider the case of two basic rotations around a common center. This situation corresponds to, for example:
  1. Two planets orbiting a star (with uniform circular motions).
  2. A planet in axial rotation geometrically orbited by a star.
  3. A planet geometrically orbited by a star and (physically) orbited by a moon.
4. Let the first rotation rate be R_1 and the second, R_2. Let the corresponding rotation periods be t_1 and t_2. Without loss of generality, we set R_1 ≥ R_2 which implies t_2 ≥ t_1.
5. The two rotating objects (e.g., planet, star, moon, reference point on a planet for an axial rotation) are separated by angle θ subtended at the common center. The initial separation angle is θ_0.
6. Let R be the relative rotation rate (i.e., the "synodic rotation rate) and t be the relative rotation period (i.e., the synodic period).
7. Note that synodic period t has been completed when θ has increased by 360° above θ_0. Thus, t satisfies:
```
  360° + θ_0 = (R_1 - R_2)*t + θ_0
  360° = (R_1 - R_2)*t  
  R = 360°/t = (R_1 - R_2)
  360°/t = (360°/t_1 - 360°/t_2)
  1/t = 1/t_1 - 1/t_2 
  t = t_1*t_2/(t_2 - t_1)  , 
```
  where the 3rd line is the formula for the relative rotation rate formula and the last line is the synodic period formula.
8. Note if R_1 < R_2, then the relative rotation is retrograde and the synodic period t < 0 (i.e., it is negative).
9. Note if R_1 = R_2, then relative rotation rate is zero and the synodic period t = ∞. In this case, the two objects corotate.
10. Note if |t_1/t_2| << 1, then we can expand the synodic period formula in a geometric series
```
  t = t_1/(1 - t_1/t_2) =  t_1*(1 +  t_1/t_2 + ...)  ,
    = t_1*(1 +  t_1/t_2) to 1st order
    = t_1*(1 +  t_1/t_2) to zeroth order  
```
  (see Wikipedia: Geometric series: Closed-form formula).
As example of the use of the synodic period formula, we can calculate the solar day = current mean value 86400.002 s which is the synodic period for two rotations the sidereal year = 365.256363004 days (J2000) the sidereal day = 86164.0905 s = 0.997269566 days = 1 day - 4 m + 4.0905 s (on average). By the formula, we get
```
  t = t_1*t_2/(t_2 - t_1) = 86399.9908 s 
```
which is only 0.011 s too small compared to the accepted value given above.
As a second example of using the synodic period formula, let's calculate the mean lunar month which is the synodic period for the Moon's orbit relative to the geometrical orbit of the Sun around the Earth. Note that the "orbital period" of the Sun around the Earth equals the true physical orbital period of the Earth around the Sun. We get
```
  t   = t_1*t_2/(t_2-t_1) = 27.321661547*365.256363004/(365.256363004-27.321661547)

      = 29.530588853 days  ,  
```
where we have used the mean sideral month = 27.321661547 days (J2000) and sidereal year = 365.256363004 days (J2000). The calculated value agrees with the accepted mean lunar month = 29.530588853 days (J2000) to 11 digit places which is all the significant figures the accepted value has.
The equation we solved for the synodic period formula is of the form
```
  0 = 1/a + 1/b + 1/c  which has solution

  a = -bc/(b + c) = -b/(1 + b/c) = to 1st order -b*(1-b/c) = to 0th order -b  , 
```
where the solutions for b and c follow by permuting the variables and where we have used the geometric series to expand in terms of small b/c (i.e., b/c << 1) (see Wikipedia: Geometric series: Closed-form formula).
Using the last item, we can now just write down the solutions for t_1 and t_2 just by permuting t, (-t_1), and t_2 in synodic period formula form
```
  t  = -(-t_1)*t_2/[t_2+(-t_1)]  .  
```
To be explicit,
```
  (-t_1)  = -t_2*t/[t+t_2]  and  t_2  = -t*(-t_1)/[(-t_1)+t]  or

  t_1  = t_2*t/[t+t_2]  and  t_2  = t*t_1/[t-t_1]  .  
```

David Jeffery

2016

Itself

local link: synodic_period.html

File

Orbit file

synodic_period.html