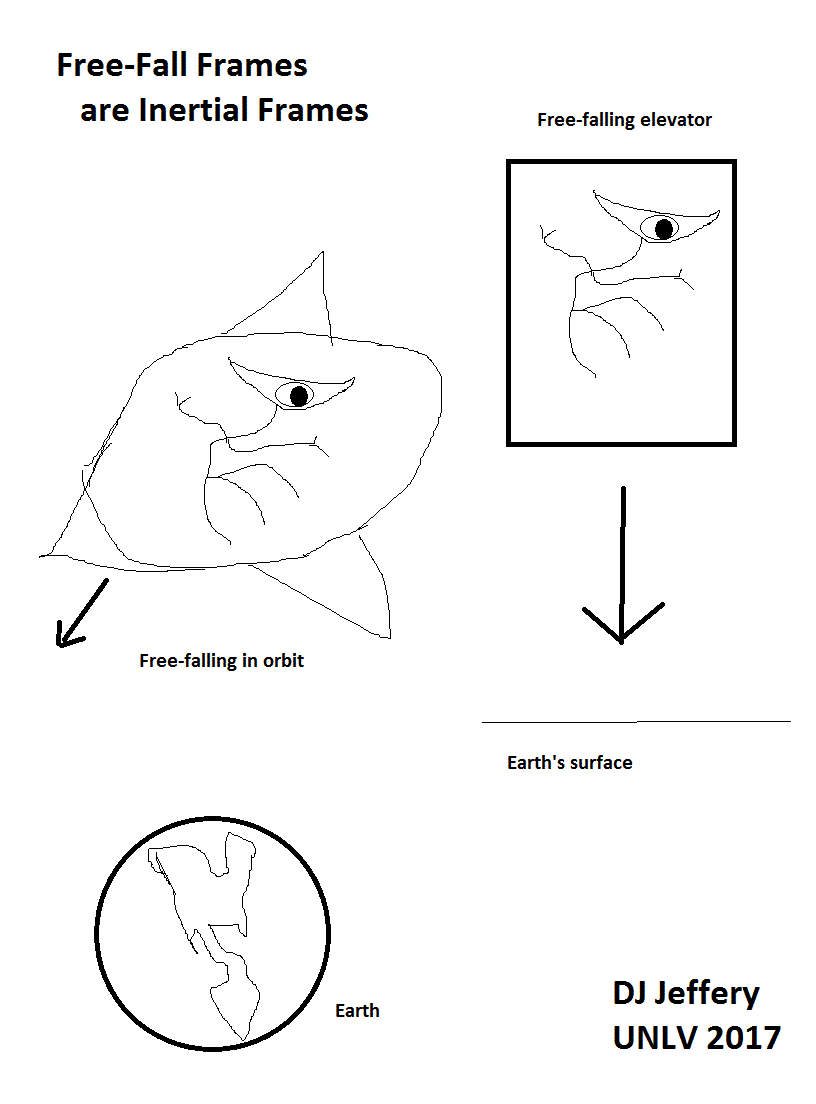
Image 1 Caption: The Alien in a free-falling elevator and a free-falling spacecraft in orbit. Both are free-falling in the sufficiently uniform gravitational field of the Earth.

Free-fall frames of reference are exact inertial frames according to general relativity. Below we explicate free-fall frames, inertial frames, non-inertial frames, and approximate inertial frames.

Explication:

1. Both the elevator and spacecraft are in free fall in a gravitational field, and so they are free-fall frames.

   Note the gravitational field is a vector field (i.e., has magnitude and direction) and is usually given the symbol "g", where the boldface indicates a vector field. When written just "g" unboldfaced, only the magnitude is meant. The gravitational field is the cause of the gravitational force: i.e., of gravity.

2. Free-fall frames are exact inertial frames. This is our modern understanding inertial frames as told to us by general relativity (GR) via the strong equivalence principle.

   The idea of inertial frames has been around ever since Newtonian physics was discovered in the 17th century by Isaac Newton (1643--1727), but the understanding of them was vague in many ways until GR was discovered. Newton hypothesized that the fundamental inertial frame was what he called absolute space which was the frame of reference in which the fixed stars (see the figure below) were at rest on average. All reference frames NOT accelerated relative to absolute space were also inertial frames. The old idea turned out to be wrong. As said above, Free-fall frames are exact inertial frames. Perhaps, we should drop the term inertial frames altogether and just use the term free-fall frames. But we have to stick with the conventional term mostly until the convention changes. Yours truly wavers back and forth between the two terms.

   ---

3. All modern physics theories (or, if you prefer, physical laws) are referenced to inertial frames, except GR itself.
   Thermodynamics (including 2nd law of thermodynamics) may also be an exception in some sense---but let's NOT worry about this fine point.

   Because physics theories are referenced to inertial frames, inertial frames have a physical nature. They are NOT just geometrical frames of reference.

   For an example of a physics theory referenced to inertial frames, consider Newtonian physics. It is a true emergent theory in the classical limit. It applies according to its rules only to inertial frames, unless you use the trick of inertial forces discussed below.

   Note Newtonian physics is NOT wrong in non-inertial frames because it is NOT referenced to non-inertial frames.

4. All reference frames NOT accelerated relative to a local inertial frame (i.e., one at the same spacetime coordinates) are also inertial frames.

   The reference frames that are accelerated relative to a local inertial frame are non-inertial frames. However, the smaller their accelerations, the better they approximate inertial frames. If a non-inertial frame has a sufficiently small acceleration for a given purpose, it can be treated as an inertial frame for that purpose.

   "Local" in physics means in the same place or nearly enough in the same place. So the local reference frames mentioned above differ in their velocities NOT in their positions.

5. In fact, non-inertial frames can also be treated like inertial frames by using the aforesaid inertial forces to deal with non-inertial frame effects. Below, we give as an example the treatment of the Earth's surface as an inertial frame using inertial forces.

6. Are there fundamental inertial frames?

   Yes. The reference frames that participate in the mean expansion of the universe are called comoving frames. The comoving frames are further explicated in the two figures below.

   ---

   ---

7. But there are obviously far more free-fall frames (i.e., exact inertial frames) than just the comoving frames.

   Virtually all astronomical objects smaller than galaxies and galaxies too when in galaxy clusters are in free fall in gravitationally-bound systems. So there is a whole hierarchy of free-fall frames (which, recall, are exact inertial frames). The hierarchy (probably NOT completely specified) is:

   1. A planet-moon system orbits its barycenter---which is usually nearly the center of the planet.
   2. A planetary system orbits its barycenter---which is usually nearly the center of the parent star.
   3. A binary star system or multiple star system orbits its barycenter---which is usually an empty point in space.
   4. A star cluster orbits its barycenter---which is usually an empty point in space.
   5. A galaxy orbits its barycenter---which is usually close to a central supermassive black hole (SMBH).
   6. A galaxy cluster or galaxy group orbits its barycenter---which is often close to a large central galaxy.

   So free-fall frames (AKA exact inertial frames) are everywhere.

   Note that the gravitationally-bound systems specified above are usually sufficiently isolated from external gravity sources that to 1st order (and often to much better accuracy/precision) the external gravity sources provide a uniform external gravitational field for the gravitationally-bound systems. This means that the internal motions of such a gravitationally-bound system in the free-fall frame of its barycenter can be determined by Newtonian physics (or general relativity if needed) just making uses of the internal gravitational fields caused by the astro-bodies of the gravitationally-bound system. This is a vast simplication since means if it you can just reference motions to the local inertial frame if that is convenient. The absolute motion of these general inertial frames (i.e., free-fall frames) relative to the identified comoving frames is easily measureable to some accuracy by ordinary astronomical observations (which we will NOT detail here).

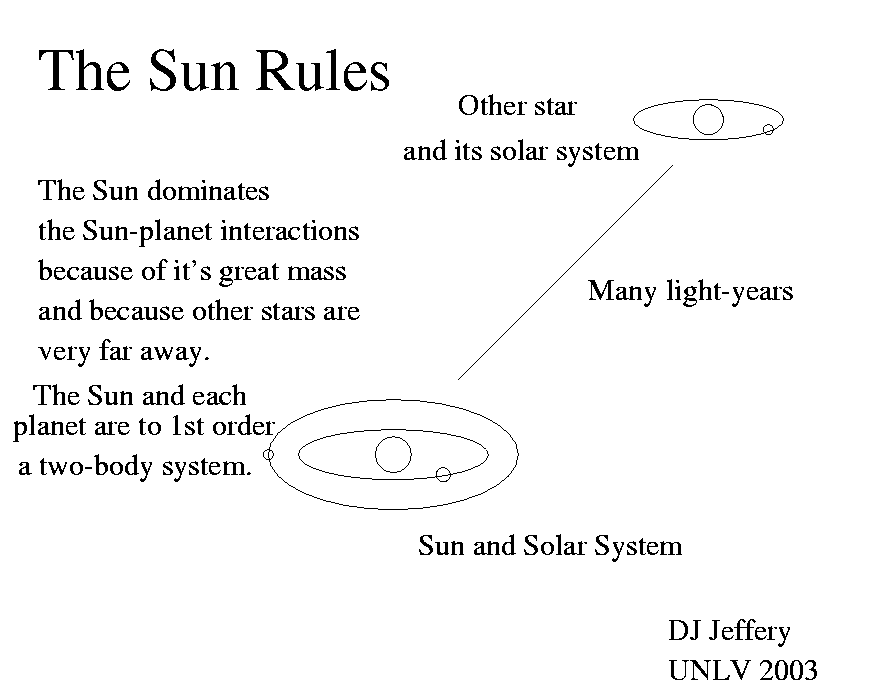
   For an important example of local inertial frame, consider the Solar System. The Solar System internal motions are to super-high accuracy/precision only determined by Solar System astro-bodies obeying Newtonian physics in the free-fall frame of the Solar-System Solar-System barycenter---which is nearly the center of the Sun since the solar mass M_☉ = 1.98855(25)*10**30 kg is 99.86 % of the Solar-System mass (see Wikipedia: Solar system: Structure and composition). Of course, the Solar-System barycenter free-fall motion itself is determined by the external gravitational field.

   The figure below illustrates the last paragraph.

   

8. Absolute Rotation Eplicated:

   Free-fall frames (i.e., exact inertial frames) do NOT rotate with respect to each other NOR the bulk mass-energy observable universe as far as we can tell.

   Note that very strong gravitational fields (like those very near black holes) may cause the rotation of free-fall frames relative to the reference frame of the observable universe, but this is a tricky point for which yours truly cannot find a clear explication. The best so far (and it does NOT say much) is Wikipedia: Inertial frame of reference: General relativity.

   The upshot is that there is an absolute rotation even though there is NO absolute space in the sense used by Isaac Newton (1643--1727).

   For clarity, yours truly usually prefers to say rotation relative to observable universe rather than absolute rotation.

   Now the fixed stars (which are just stars relatively near the Sun inside the Milky Way) have very small rotation relative to observable universe, and so one traditionally says rotation relative to the fixed stars meaning absolute rotation. This has been true through history since the idea of inertial frames was introduced by Newton.

   In fact, to good accuracy/precision, all one needs is to measure rotation relative to the fixed stars. For most purposes, the fixed stars define a good-enough inertial frame.

   Yours truly often says/said rotation relative to the fixed stars. Probably this usage should be phased out now that we know what absolute rotation is for the observable universe.

   Note, however, the fixed stars are rotating to some degree with respect to their barycenter (which is hard to locate and depends on which fixed stars you include in your determination), and so rotation measurements with respect to the fixed stars do NOT give absolute rotation to super-high accuracy/precision by modern standards. For super-high accuracy/precision, one measures rotation relative to cosmologically remote quasars and galaxies whose peculiar velocities (i.e., velocities relative their comoving frame) give very negligible angular velocities because of their remoteness, and thus they exhibit zero absolute rotation to very high accuracy/precision. In a sense, the fixed stars are replaced by the "fixed galaxies and quasars."

   Note that beyond the observable universe, one may need a different more fundamental definition of absolute rotation, but we do NOT know what that is.

9. Having the idea of free-fall frames and their zero absolute rotation gives the definition of physical orbits (i.e., usually orbits without qualification) as opposed to geometrical orbits.

   The distinction is NOT the shape NOR kinematics of the orbits, but whether these follow directly from an application of Newtonian physics (or general relativity if needed) to a gravitationally bound system.

   If the orbit does so follow, it is a physical orbit and if NOT it is a geometrical orbit. So it is a matter of perspective rather than shape and kinematics.

   But the perspective is important since inertial frame allows you to directly calculate and understand the orbit, and other reference frame do NOT in a direct sense.

   In indirect way, one can calculate an orbit for any reference frame, but "indirect way" is is the same as saying you are switching to an inertial frame implicitly in some way.

   The center of the orbits of a gravitationally bound system is its center of mass which is called barycenter when applied to a gravitationally bound system.

   If the barycenter of the gravitationally bound system rouphly corresponds to the most massive astro-body of the system, then we can say that to 1st order the other astro-bodies orbit the most massive astro-body.

   Examples of such systems:

   1. The Moon orbits the Earth.
   2. The Earth orbits the Sun.
   3. The Sun orbits the Milky Way barycenter which is very near Sagittarius A* (Galactic central black hole).
   4. The Milky Way orbits the barycenter of the Local Group (which is very poor galaxy cluster).

   Note that using the center of the Earth as the center of geometrical orbits is often a useful observational perspective as shown by all of the history of astronomy.

10. Physical rotation is even easier to understand than physical orbits: it is rotation relative to the observable universe.

    So the Earth physically rotates relative the observable universe, but the observable universe (and so the celestial sphere) only geometrically rotates around the Earth.

    The rotation of the follows from the application of Newtonian physics to the Solar System.

11. Reference frames rotating relative to the observable universe (e.g., the surfaces of moons, planets, stars, etc.) CANNOT be exact inertial frames since every point in them is accelerating relative some local inertial frame.

    However, if the acceleration is low enough, the rotating reference frame may be a sufficiently inertial frame for many purposes.

    The tidal force is another complication in treating rotating reference frames as sufficiently inertial frame for many purposes.

12. To explicate rotating reference frames sufficiently inertial frames, let's consider the important example of the Earth. Other rotating astro-bodies can be explicated similarly, mutatis mutandis.

    The Earth's center of mass is in the free-fall frame of the gravitational field provided by, in decreasing order of importance and increasing order of uniformity, the Moon, the Sun, Milky Way, and the rest of the universe (or our pocket universe if that is a true theory).

    So the center-of-mass frame is an inertial frame. However, the surface of the Earth is accelerated relative to the center-of-mass frame by the Earth's rotation. In one sense, the Earth's rotation is fast: ranging from 0 at the poles to 0.46510 km/s at the equator (see Wikipedia: Earth's rotation: Angular speed). However, the centripetal acceleration of the Earth's rotation ranges from 0 at the poles to only ∼ 0.05 m/s**2 at the equator (see Wikipedia: Gravity of Earth: Latitude) which is much smaller than Earth's gravitational field strength g = 9.8 N/kg = 9.8 m/s**2 (fiducial value) (which is the relevant comparison: see just below).

    The centripetal acceleration in fact is treated by inertial forces, the centrifugal force and the Coriolis force. The centrifugal force just reduces the effective Earth's gravitational field: by 0 at the at the poles to ∼ 0.05 N/kg = 5 m/s**2 at the equator (see Wikipedia: Gravity of Earth: Latitude). The reduction is below human perception, but is quite easily measured by, e.g., a gravimeter. The Coriolis force is important for helping to determine atmospheric circulation and affects long-range artillery. However, on the human size scale, the Coriolis force is negligible.

    Besides non-inertial frame effects, the Earth is affected by the tidal force of the Moon and to a smaller amount that of the Sun. The tidal force is just a stretching force due to the variation in the gravitational field: i.e., its non-uniformity. The tidal force is important for the tides, but on the human size scale it is negligible.

    The upshot of the foregoing is that the Earth's surface is a sufficiently inertial frame for most purposes and when it is NOT you account for non-inertial frame effects with inertial forces.

    Similarly for reference frames unaccelerated relative to the Earth's surface: e.g., unaccelerated planes, trains, and automobiles.

    Note that Newtonian physics would NOT be much use in everyday life if we could NOT treat the surface of the Earth as an approximate inertial frame for most purposes.

13. The non-rotation of free-fall frames (i.e., an exact inertial frame) relative to the observable universe (or the fixed stars to usually sufficiently good accuracy/precision) can be observed on Earth with a Foucault pendulum. See the figure below (local link / general link: pendulum_foucault.html).

Images:

1. Credit/Permission: © David Jeffery, 2017 / Own work.
   Image link: Itself.
   
2. Credit/Permission: © David Jeffery, 2003 / Own work.
   Image link: Itself.