Features:

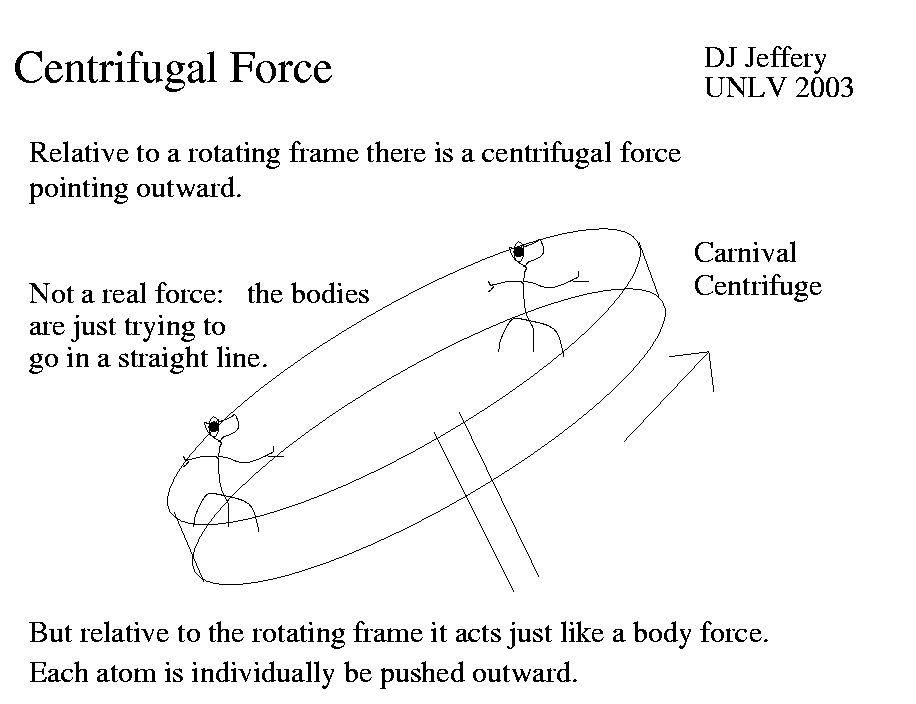
1. Image 1 Caption: The centrifugal force on a carnival centrifuge.
   Question: If you swirl a bottle of water:
   1. the water surface stays parallel to the ground.
   2. the water surface rises TOWARD the center of the circular motion.
   3. the water surface rises AWAY from the center of the circular motion.

   
   
   Answer 3 is right.

   In order to move in a circle there must be a centripetal force.

   The wall of the bottle provides this only for the fluid touching the wall.

   In the interior this force must be provided by pressure. So pressure must increase with radius from the center of the circular motion.

   But this variation in pressure with radius forces a variation in the vertical colummn height with radius.

   Low pressures at small radius can only support a low level of water; high pressures at large radius support a high level of water.

   One can view the situation from the ROTATING FRAME treated as an inertial frame with the centrifugal force treated as a real force.

   In this picture, the water just seeks a hydrostatic equilibrium configuration with centrifugal force, pressure force, and gravity canceling at every point.

   The shape of the surface for hydrostatic equilibrium in the rotating frame is, in fact, parabolic (Fre-550).

   If one just as a rotating glass of water a similar analysis holds. See the figure below.

   

2. Image 2 Caption: A rotating glass of water.

Images:

1. Credit/Permission: © David Jeffery, 2003 / Own work.
   Image link: Itself.
   
2. Credit/Permission: © David Jeffery, 2004 / Own work.
   Image link: Itself.