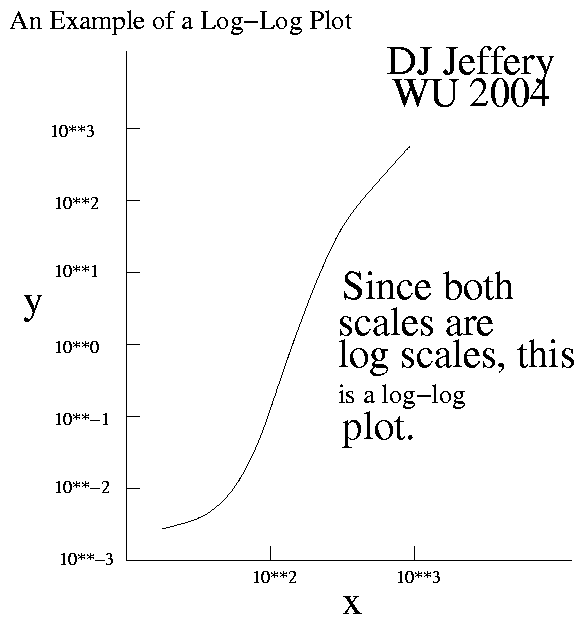
Caption: An example of a log-log plot.
Features:
- Logarithmic plots
are where one or both
axes are
logarithmic.
If both are, it is
a log-log plot;
if only one, it is a
semi-log plot.
You do NOT have to know what a logarithm is to appreciate log plots. In fact, you quickly develop an intuitive understanding of them.
- Logarithmic plots
are useful for showing a
function over many
orders of magnitude
by allowing you to see the functional behavior on many scales simultaneously.
The cost of logarithmic plots is that functions are a bit distorted by linear-scale standards. But, in fact, there is NOT much cost because you usually quickly develop an intuitive understanding of them.
- Logarithmic plots
achieve their many-scales effect
by having
tick marks the on axes
separated by
factors
(usually
powers of
10) of a
quantity and NOT constant
amounts of the quantity.
In logarithmic plots jargon one power of 10 is called a dex.
- To explicate further,
on linear-scale plots,
much of the behavior of a
function
that varies tremendously with scale
(like the function in the image)
is off the plot
or is squashed down to the
x-axis and/or
y-axis.
Many linear-scale plots may be needed to show the whole functional behavior in roughly equal detail.
- For example for the function
in the image,
if you displayed the whole function
on a linear-scale plot,
all the lower left behavior would be squashed into the
x-axis and
y-axis,
and would be invisible or nearly invisible.
The log-log plot allows us to see that behavior easily.
EOF
Credit/Permission: ©
David Jeffery,
2004 / Own work.
Image link: Itself.
Local file: local link: log_log_plot_dj.html_plot.html.
Extended file: Mathematics file:
log_log_plot_dj_4.html.
File: Mathematics file:
log_log_plot_dj.html.