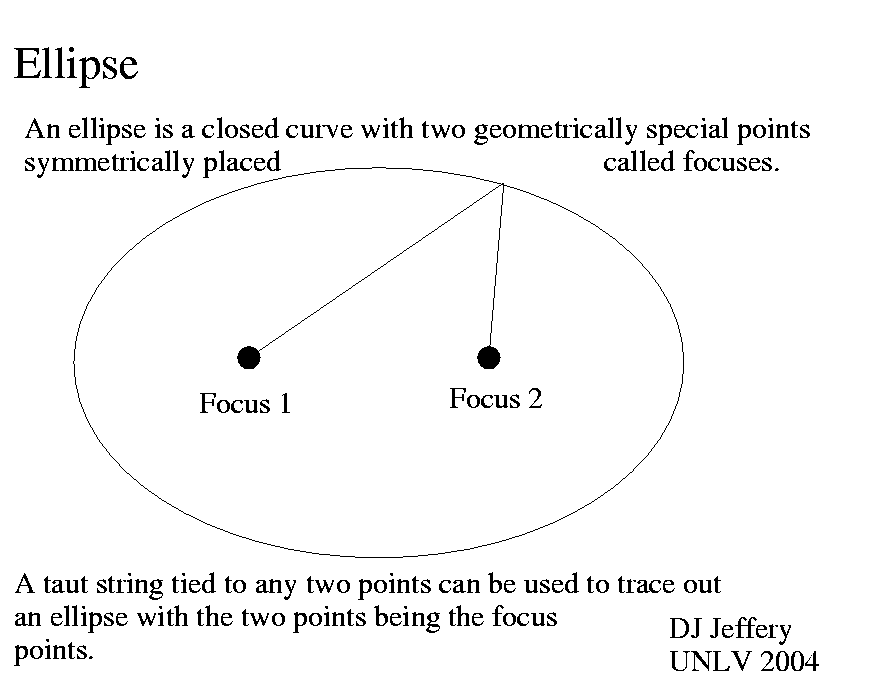
Caption: Ellipse diagram showing the two focuses---which are special points of an ellipse that enter into ellipse formulae and into the geometrical contruction of ellipses.

Features:

1. The formula for an ellipse in 2-dimensional x-y Cartesian coordinates is

     (x/a)**2+(y/b)**2=1  , 

   where the origin is at the geometric center of the ellipse (i.e., the point of highest symmetry), a is the semi-major axis (i.e., half the long axis aligned with the x-axis), b is the semi-minor axis (i.e., half the short axis aligned with the y-axis), and a ≥ b without loss of generality since one can just flip the names if a < b and rotate the ellipse by 90°.

   If a = b, then the ellipse specializes to the circle with radius a = b.

2. For a geometrical construction of an ellipse, stick two pins in a sheet of paper with a loose string between them. Hold the string taut with a pencil and move the pencil all around the pins. The pencil will trace out an ellipse. The two pin points are the ellipse focuses.

   Proving this geometrical construction is consistent with the x-y formula above takes a bit of work. We do this in the Extended Features of the Extended File: Mathematics file: ellipse_4.html---which if this file is that file, we do the work below.

3. There's a formula for showing how ellipses elongated with a parameter called eccentricity, but we will NOT show it---we I don't what to shock and awe the students.

4. But qualitatively how eccentricity controls ellipse elongation.

   First note that usually eccentricity is given the symbol e---NOT to be confused with the exponential e.

   Fiducial values of eccentricity e are:

   1. e = 0 for a circle.
   2. e ∈ (0,1) for a non-circular ellipse.
   3. e = 1 for an ellipse stretched into a line segment.