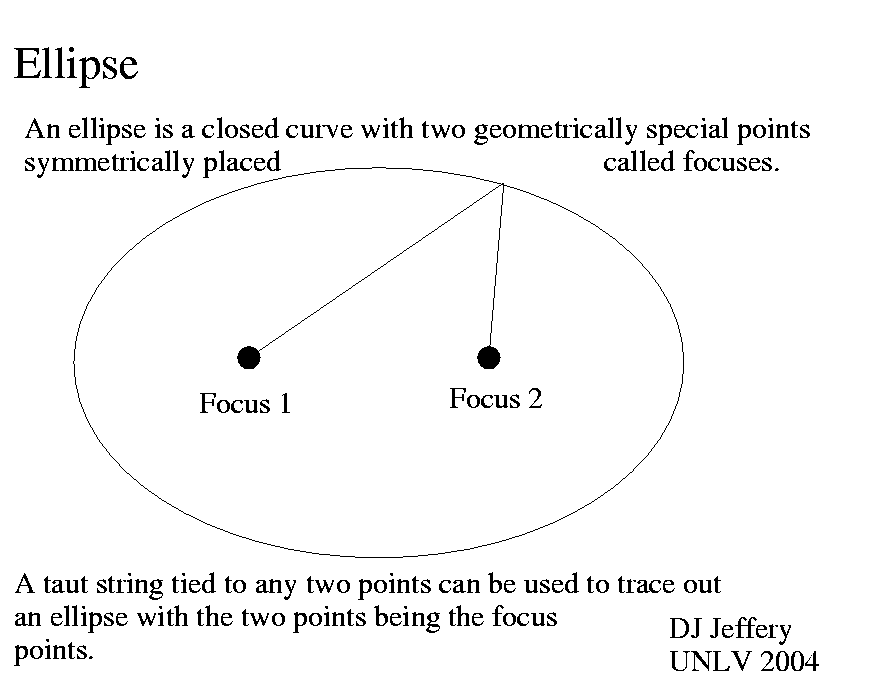
Caption: An Ellipse diagram showing the 2 focuses---which are special points of an ellipse that enter into ellipse formulae and into the geometrical contruction of ellipses.

Features:

1. The formula for an ellipse in 2-dimensional x-y Cartesian coordinates is

     (x/a)**2+(y/b)**2=1  , 

   where the origin is at the geometric center of the ellipse (i.e., the point of highest symmetry), "a" is the semi-major axis (i.e., half the long axis aligned with the x-axis), "b" is the semi-minor axis (i.e., half the short axis aligned with the y-axis), and a ≥ b without loss of generality since one can just flip the names if a < b and rotate the ellipse by 90°.

   If a = b, then the ellipse specializes to the circle with radius a = b.

2. For a geometrical construction of an ellipse, stick 2 pins in a sheet of paper with a loose string between them. Hold the string taut with a pencil and move the pencil all around the pins. The pencil will trace out an ellipse. The 2 pin points are the ellipse focuses.

   Proving this geometrical construction is consistent with the x-y formula above takes a bit of work. We do this in the Extended Features of the Extended File: Mathematics file: ellipse_4.html---which if this file is that file, we do the work below.

3. There's a formula for showing how ellipses elongate with a parameter called eccentricity, but we will NOT show it---we don't what to shock and awe the students.

4. But qualitatively how does eccentricity control ellipse elongation?

   First note that usually eccentricity is given the symbol e---NOT to be confused with the exponential e.

   Fiducial values of eccentricity e are:

   1. e = 0 for a circle.
   2. e ∈ (0,1) for a non-circular ellipse.
   3. e = 1 for an ellipse stretched into a line segment.

5. Note that you can also express eccentricity as a percentage: i.e.,

            e_prct = (100*e) %  . 

   The percentage form is often clearer when speaking of eccentricity.