Crystal Structure Prediction and its Application in Earth and Materials Sciences: MgSiO

3.2 MgSiO $_3$

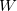We also checked that the approach presented here correctly reproduces the previous results on pressure-induced transitions in MgSiO $_3$ ¹⁷¹ (see Fig. 8.3). In this calculation, we set Gaussian parameters $W$ =7000 kbar 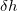$\cdot$ $^3$ , $\delta {h}$ =0.8 , and 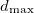$d_{\rm max}$ =3.0 . Structures were relaxed using the GULP code with a partially ionic Buckingham potential ²²⁷. Our calculation found the transition from perovskite to post-perovskite, and structures b, c, d were also observed in the simulation. Plane sliding with the formation of stacking faults is a possible pathway for this phase transition, in accordance with the previous metadynamics study ²²⁰.

$\includegraphics[scale=0.7]{chapter8/pdf/Fig3.png}$

Figure 8.3: Phases observed in evolutionary metadynamics starting from a 160-atom supercell of perovskite (MgSiO $_3$ ) at 250 GPa. (a) perovskite (space group Pbnm); (b) 2 $\times$ 2 phase (Pbnm); (c) 3 $\times$ 1 phase (P2 $_1$ /m); (d) 4 $\times$ 4 phase (Pm); (e) post-perovskite (Cmcm). Only Si octahedra are shown (Mg atoms are omitted for clarity).

After these successful tests, we applied it to two challenging and important problems, namely the pressure-induced transformations of elemental carbon and Al2 SiO5 . Modified formalism based on Eq. 6 gives very similar results, but is invariant to the choice of supercell and more efficient.