3.1 SiO

Below we discuss results obtained with Eq. (2) and Eq. (3), i.e. the original and simplest formulation of metadynamics ²²⁴ with isotropic Gaussians. In reality, the FES minima are anisotropic - the local FES curvature is lower for shear and higher for compressional distortions of the cell. It was found that the "isotropic" formalism based on Eq. (3) coupled with MD equilibration is incapable of predicting structural transformations of silica and gets stuck in amorphization ²²⁰. This problem was remedied by the anisotropic extension of Eq. (3) ²²⁰. Here we find that this increase of complexity can be avoided and the same structural transformations are easily predicted with the isotropic formulation of metadynamics, if softmutation is used instead of MD for equilibration (see Fig. 8.2). In this calculation, we set Gaussian parameters 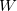=10000 kbar, 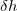=1.0 , and 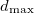=3.0 . Each generation contains 40 structures. Structures were relaxed using the GULP code with the BKS potential ²²⁶. We first observed the transition from -quartz (space group P321) to quartz II (C2) in the 9th generation, and then quartz II amorphized until it transformed into the anatase structure (I4/amd) in the 22th generation. Anatase amorphized again, and evolved into the 3 2 P2/c structure in the 58th generation, and then transformed into stishovite (P4/mnm) at the 69th generation.

Figure 8.2: Enthalpy evolution during the compression on 72-atom supercell of -quartz (SiO) at 10 GPa (black line: enthalpies for best structures with constant h; magenta line: enthalpies for best structures after full relaxation).