2 Methodology

MD method is widely used to study physical processes in liquids and solids ²²¹, but has difficulties in escaping from local energy minima and crossing high energy barriers ²²². Metadynamics ²¹⁹ is an ingenious way to solve this problem and accelerate the activated processes involving barrier crossing, including first-order reconstructive transitions. In metadynamics, one has to specify collective variables that adequately describe the evolution of the system, and then perturb the FES defined in this reduced space of collective variables. Martonak et al. used the cell box h (3 $\times$ 3 matrix) as a collective variable to distinguish different structures ⁷. For a given system with volume V under external pressure P, the derivative of the free energy G with respect to h is

$\begin{equation} \label{eq:Gibbs1} -\frac{\partial G}{\partial h_{ij}} = V[h^{-1}(P-p)]_{ji} \end{equation}$

(1)

where p is the internal pressure tensor calculated for each given geometry.

The collective variable evolves with a stepping parameter 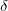$\delta$ h,

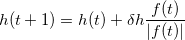$\begin{equation} \label{eq:tensor} h(t+1) = h(t) + \delta {h}\frac{f(t)}{|f(t)|} \end{equation}$

(2)

here the driving force 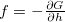$f = -\frac{\partial G}{\partial h}$ is from a history-dependent Gibbs potential 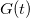$G(t)$ where a Gaussian has been added to 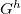$G^ h$ at every point 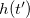$h(t’)$ already visited in order to discourage it from being visited again,

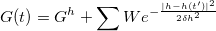$\begin{equation} \label{eq:Gibbs} G(t) = G^ h + \sum We^{-\frac{|h-h(t')|^2}{2\delta {h^2}}} \end{equation}$

(3)

As the simulation proceeds, the history-dependent term fills the initial well of the FES, and concurrently the collective variables (the cell) undergo a sequence of changes, at each of which the atoms are re-equilibrated. At some critical cell distortion atoms rearrange dramatically, yielding a new crystal structure.

By adding a history-dependent Gaussian potential, metadynamics efficiently reaches and crosses the transition state, thus solving an intrinsic problem of MD simulations. However, it still relies on the ability of MD to equilibrate the system at each value of collective variables. Metadynamics encounters two general problems. First, MD is not a very efficient technique for equilibration involving crossing energy barriers, especially at low temperatures. Second, metadynamics reduces the full energy landscape to a low-dimensional projection, which is not always adequate.

For a crystal with N atoms in the unit cell, the number of degrees of freedom is 3N+3. Metadynamics assumes that the system can be described by 6 collective variables representing the box h. The remaining 3N-3 dimensions describe atomic positions, and we need to determine the global energy minimum with respect to these dimensions at given h. This can be done using MD (as in standard metadynamics), but as discussed above, this encounters certain problems. Here we do it using global optimization techniques based on evolutionary algorithms ^{4; 23; 79}. These algorithms use several variation operators - i.e. recipes for obtaining new structures from the previously sampled ones - for sampling the energy landscape. Here we use the softmutation operator ⁷⁹, which connects global optimization with lattice dynamics and group theory. Indeed, the 3N-3 variables describing atomic positions can be transformed into a set of normal modes that possess valuable properties. If a structure is not dynamically stable, a more stable structure is obtained by following the eigenvector of the softest vibrational mode. For structures without soft modes, there is a statistically valid Bell-Evans-Polanyi principle that states that low-energy structures are usually connected by low activation barriers ³⁴. Low barriers are, in turn, usually related to the direction of the lowest curvature of the FES - or eigenvectors of the softest vibrational mode. This is the principle behind the minima hopping method ¹⁰ and explains the efficiency of the softmutation operator introduced in the evolutionary algorithm USPEX ⁷⁹. To calculate the vibrational modes, we construct the dynamical matrix from bond hardness coefficients.

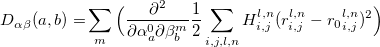$\begin{equation} \label{eq:dynamical matrix} \begin{aligned} D_{\alpha \beta }(a,b) = & \sum _ m \Big(\frac{\partial ^2}{{\partial \alpha _ a^0}{\partial \beta _ b^ m}} \frac{1}{2} \sum _{i,j,l,n} H_{i,j}^{l,n}(r_{i,j}^{l,n}-{r_{0}}_{i,j}^{l,n})^2\Big) \end{aligned} \end{equation}$

(4)

Here coefficients 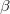$\alpha$ , $\beta$ denote coordinates 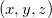$(x,y,z)$ ; coefficients 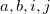$a, b, i, j$ describe the atom in the unit cell; coefficients 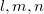$l, m, n$ describe the unit cell number; 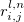$r_{i,j}^{l,n}$ is the distance between atom $i$ in the unit cell 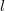$l$ and atom 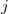$j$ in the unit cell 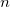$n$ , while 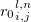${r_{0}}_{i,j}^{l,n}$ is corresponding bond distance, and 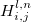$H_{i,j}^{l,n}$ is bond hardness coefficient computed from bond distances, covalent radii and electronegativities of the atoms ^{79; 223}.

To perform softmutation, we move the atoms along the eigenvector of the softest calculated mode. One structure can be softmutated many times using different non-degenerate modes and displacements. By properties of normal modes, the original and softmutated structures are linked by group-subgroup symmetry relations, but structure relaxation may result in a symmetry increase. In this case one observes a structural transition with a common subgroup. The magnitude of the displacement (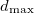 $d_{\rm max}$ ) along the mode eigenvector is an input parameter: with relatively small 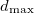$d_{\rm max}$ and displacements represented by a random linear mixture of all mode eigenvectors, we obtain a method similar to MD-metadynamics in its ability to cross energy barriers and equilibrate the system. With large 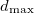$d_{\rm max}$ along the softest mode eigenvectors, we obtain the softmutation operator ⁷⁹, capable of efficiently finding the global energy minimum. When needed, other evolutionary variation operators can be used - such as permutation (swaps of atomic identities) or heredity (combination of pieces of two parent structures).

Our algorithm as shown in Fig. 3.1 is in many ways similar to the original version by Martonak et al. ²²⁴. We start from one known initial structure at a given external pressure P, and then compute its vibrational modes, which are used to produce typically 20-40 softmutated structures. These are relaxed at constant h, the lowest-enthalpy structure is selected and its pressure tensor p is computed. Its box h is then updated according to Eq. (2), and a new generation of softmutated structures are produced and relaxed in the fixed cell h. Repeated for a number of generations, this computational scheme leads to a series of structural transitions and is stopped when the maximum number of generations is reached. Due to the presence of a population of structures and a selection step, this algorithm is evolutionary, unlike original metadynamics ²²⁴.

$\includegraphics[scale=0.7]{chapter8/pdf/Fig1.png}$

Figure 8.1: Illustration of the evolutionary metadynamics algorithm.

In addition to 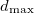$d_{\rm max}$ , there are two other important parameters - the Gaussian height ( 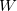$W$ ) and Gaussian width ( 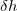$\delta {h}$ ), for choosing which Martonak et al. ²²⁴ proposed a recipe based on the curvature of the FES at the minimum. According to our experience, a good starting point is to set 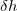$\delta {h}$ as one tenth of the minimum lattice vector, and 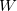$W$ as around 8,000 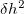$\delta {h}^2$ (with the unit of kbar $\cdot$ $^3$ ).

Note that Eq. (2) is not invariant with respect to the choice of the unit cell (or supercell) and works best for cells close to cubic shape. To remedy this, we developed a more sophisticated equation based on elasticity theory,

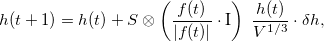$\begin{equation} \label{eq:newtensor} h(t+1) = h(t)+ S \otimes \left(\frac{f(t)}{|f(t)|} \cdot {\bf \text I} \right) ~ \frac{h(t)}{V^{1/3}} \cdot \delta h, \end{equation}$

(6)

where I is the unit stress matrix. Here we use the elastic compliance tensor (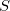 $S$ ) corresponding to an elastically isotropic medium with Poisson ratio ( $\nu$ ) of 0.26, which corresponds to the border between brittle and ductile materials ²²⁵ and is a good average value to describe both metals and insulators. The choice of the Poisson ratio does not significantly affect the results; the main effect of Eq. (6) is to make the results independent of the simulation cell shape. The Young’s modulus is chosen in such a way that for a cubic cell under uniform stress the original formula Eq. (2) is reproduced. We have implemented and tested the formalism based on Eq. (6) and found it to work extremely well, the efficiency improves compared to Eq. (2).