2 Methodology

Compared to the prediction of atomic structures, there are several features to be taken into account for molecular crystals:

i) A typical unit cell contains many more atoms than a normal inorganic structure, which means an explosion of computing costs if all of these atoms are treated independently;

ii) Molecules are bound by weak forces, such as the vdW interactions, and the inter-molecular distances are typically larger than those in atomic crystals, which leads to the availability of large empty space;

iii) Most of the molecular compounds are thermodynamically less stable than simpler molecular compounds from which they can be obtained (such as HO, CO, CH, NH, H). This means that a fully unconstrained global optimization approach in many cases will produce a mixture of these simple molecules, which are of little interest to the organic chemists. To study the packing of the actual molecules of interest, it is necessary to fix the intramolecular connectivity;

iv) Crystal structures tend to be symmetric, and the distribution of structures over symmetry groups is largely uneven ⁸⁰. For example, 35% of inorganic and 45% of organic materials have the point group 2/m. Compared to inorganic crystals, there is a strong preference of organic crystals to a small number of space groups. Over 80% of organic crystals are found to possess space groups: P2/c (36.59%), P-1 (16.92%), P222 (11.00%), C2/c (6.95%), P2 (6.35%) and Pbca (4.24%) ⁸¹.

The first two points indicate that the search space is huge. If we start to search for the global minimum with randomly generated structures, it is very likely that most of the time will be spent on exploring those uninteresting disordered structures far away from the global minimum. Fortunately, the last two points suggest a way to improve the efficiency. The point (iii) implies that the true thermodynamic ground state corresponding to most organic compositions is a mixture of simpler molecules, which is of little interest to the organic chemists. The truly interesting problem, packing of the pre-formed molecules, can be solved by constrained global optimization – finding the most stable packing of molecules with fixed bond connectivity. This will not only make the global optimization process meaningful, but at the same time will simplify it, leading to a drastic reduction of the number of degrees of freedom and of the search space. Structure prediction (global optimization) must involve relaxation (local optimization) of all structures, and fixing intra-molecular bond connectivity has an added benefit of making structure relaxations cheaper and more robust. Depending on their chemical nature, those molecules shall be treated as fully or partly rigid bodies during the action of evolutionary variation operators and local optimization. Another improvement of the efficiency is achieved by using symmetry in the random generation of new structures - a population of symmetric structures is usually more diverse than a set of fully random (often disordered) structures. Diversity of the population of structures is essential for the success and efficiency of evolutionary simulations.

We have successfully implemented the adapted evolutionary algorithm in the USPEX code. Briefly, our procedure is as follows (as shown in Fig. 3.1).

Figure 3.1: Illustration of the constrained evolutionary algorithm.

Figure 3.2: Illustration of the variation operators: a) heredity; b) coordinate mutation; c) rotational mutation.

1) The initial structures are usually generated randomly, with randomly selected space groups. First, we randomly pick one of 230 space groups, and set up a Bravis cell according to the per-specified initial volume with random cell parameters consistent with the space group. Then one molecule is randomly placed on a general Wyckoff position, and is multiplied by space group operations. If two or more symmetry-related molecules are found close to each other, we merge them in one molecule that sits on a special Wyckoff position and has averaged coordinates of the molecular center and averaged orientational vectors (or random, when the average vector is zero). Adding new molecular sites one by one, until the correct number of molecules is reached, we get a random symmetric structure. During this process, we also make sure that no molecules overlap or sit too close to each other. All produced unit cell shapes are checked and, if necessary, transformed to maximally orthogonal shapes ²⁷.

Figure 3.3: Illustration of the symmetrization. For a given space group randomly assigned by the program, the Bravis cell and Wyckoff positions are generated. Molecules are then constructed around the Wycoff positions according to the symmetry operations. If the high symmetrical Wyckoff sites are involved, the generated structures are likely to dissatisfy the symmetry operations and thus it only has subgroup symmetries.

2) Structural relaxation is done stepwise from low to high precision. At the initial stages, we employ the SIESTA code ⁶⁵ for first-principles simulations, which allows the constrained geometry relaxation. As an option, we can use the DMACRYS code ⁶³ for classical calculations. We note that SIESTA provides Z-matrix representation for the molecules⁸², enabling the specification of the molecular geometry and its internal degrees of freedom (important when dealing with conformationally flexible molecules). For the final stages of relaxation, we can keep the molecules fully or partly rigid, or allow their complete relaxation (in the latter case, such codes as GULP and VASP are also supported in USPEX). It is a good strategy to relax the structures in SIESTA with constrained molecular geometry at the beginning stage and then fully relax them using VASP, and here we adopt this strategy. It is well known that DFT within local and semi-local approximations, such as the LDA or GGA, cannot describe vdW dispersion interactions well (e.g., ⁸³), and we therefore used the GGA+D approach that includes a damped dispersion correction ⁵¹; this approach is known to work well for molecular crystals.

3) At the end of each generation, all structures in the generation are compared using their fingerprints ²⁸ and all non-identical structures are ranked by their (free) energies or enthalpies. There is an important technical aspect: intramolecular contributions are identical for all different packings of the same molecule and thus decrease the discriminatory power of the fingerprint function. Therefore, we remove the intramolecular distances from the computation of the fingerprint function when dealing with molecular crystals.

A certain percentage of higher-energy structures in the population are discarded, and the rest participate in creating the next generation using variation operators detailed below.

To ensure properly constrained global optimization, we not only generate the structures made of the desired molecules, but also check that the bond connectivity has not changed after relaxation - structures with altered connectivity graphs are discarded.

4) Child structures (new generation) are produced from parent structures (old generation) using one of the following variation operators: (i) heredity, (ii) permutation, (iii) coordinate mutation are the same as in atomic crystal structures ^{4; 79}, with the only difference that variation operators act on the geometric centers of the molecules and their orientations, i.e. whole molecules, rather than single atoms, are considered as the minimum building blocks. Since molecules cannot be considered as spherically symmetric point particles, additional variation operators must be introduced: (iv) rotational mutation of the whole molecules, (v) softmutation - a hybrid operator of coordinate and rotational mutation. Fig. 3.3 shows how variation operators work in our algorithm. Below we describe how these variation operators were used in our test cases.

Heredity: This operator cuts planar slices from each individual and combines these to produce a child structure. In heredity, each molecule is represented by its geometric center (Fig. 3.3a) and orientation. From each parent, we cut (parallel to a randomly selected coordinate plane of the unit cell) a slab of random thickness (within bounds of 0.25-0.75 of the cut lattice vector) from a random height in the cell. If the total number of molecules of each type obtained from combining the slabs does not match the desired number of molecules, a corrector step is performed: molecules in excess are removed while molecules in shortage are added; molecules with higher local degree of order have higher probability to be added and lower probability to be removed. This is equivalent to our original implementation of heredity for atomic crystals⁴

Permutation: this operator swaps chemical identity in randomly selected pairs of molecules.

Coordinate mutation: All the centers of molecules are displaced in random directions, the distance for this movement for molecule i being picked from a zero-mean Gaussian distribution with defined as:

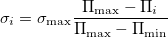(1)

where is the local order of the molecule. Thus molecules with higher order are perturbed less than molecules with low order (Fig. 3.3b). We calculate the local order parameter of each molecule from its fingerprint ²⁸, in the calculation of which only centers of all molecules are used. In the tests described here we use of the order of a typical intermolecular distance.

Rotational mutation: A certain number of randomly selected molecules are rotated by random angles (Fig. 3.3c). For rigid molecules, there are only 3 variables to define the orientation of the molecules. For flexible molecules, we also allow the mutation of torsional angles of the flexible groups. A large rotation can have a marked effect on global optimization, helping the system to jump out of the current local minimum and find optimal orientational ordering.

Softmutation: This powerful operator, introduced first for atomic crystals ⁷⁹, involves atomic displacements along the softest mode eigenvectors, or a random linear combination of softest eigenvectors. In the context of molecular crystals it becomes a hybrid operator, combining rotational and coordinate mutations. In this case, the eigenvectors are calculated first, and then projected onto translational and rotational degrees of freedom of each molecule and the resulting changes of molecular positions and orientations are applied preserving rigidity of the fixed intramolecular degrees of freedom. To calculate efficiently the normal modes, we construct the dynamical matrix from bond hardness coefficients ⁷⁹. The same structures can be softmutated many times, each time along the eigenvector of a new mode.

At the end of the selection, the best individuals in the last generation (usually up to 5) are kept. To maintain diversity of the population, some fraction (usually 15% - 30%) of population is randomly generated with symmetry. While simple random generation does not improve diversity, the use of symmetry does allow a diverse set of structures to be produced.

5) The simulation is stopped once a predefined halting criterion is met. The lowest-energy structures found in USPEX are then carefully relaxed with higher precision using the same level of theory: the all-electron projector-augmented wave (PAW) method ⁵⁷, as implemented in the VASP code, at the level of generalized gradient approximation (GGA) ⁴³ for inorganic systems; or dispersion-corrected GGA+D ⁵¹ approximation for organic crystals. We used the plane wave kinetic energy cutoff of 550 eV and the Brillouin zone was sampled with a resolution of 2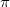 0.07 , which showed excellent convergences of the energy differences, stress tensors and structural parameters.