| Crystal Structure Prediction and its Application in Earth and Materials Sciences |
To solve the equation 60, the most direct approach is simply to calculate the total energy and forces as a function of the position of nuclei, i.e. ‘frozen phonons’. Then the relevant quantities (most importantly, force constant matrix) are constructed by the displacements:
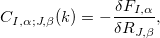 |
(61) |
Such calculations are widely used since they require no additional computational algorithms. It is also mainly used in this thesis by using the Phonopy code 67. However, I would like to note that one has to make sure that the interactions between atomic pairs are adequate. Practically, one can build one super cell to give phonons at all wave vectors. The results are limited to small super cells. For instance, one only need a primitive cell to calculate the the  -point. If we want the entire dispersions for all vectors in BZ, a more accurate model should be proposed, for instance density functional perturbation theory 68
-point. If we want the entire dispersions for all vectors in BZ, a more accurate model should be proposed, for instance density functional perturbation theory 68