Crystal Structure Prediction and its Application in Earth and Materials Sciences: Lattice dynamics and phonons

3.1 Lattice dynamics and phonons

To understand the motion of atoms, we need first know the force:

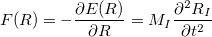$\begin{equation} \label{eq:force} F(R) = -\frac{\partial {E(R)}}{\partial R} = M_ I \frac{\partial ^2{R_ I}}{\partial t^2} \end{equation}$

(55)

For stable solids at some temperature, it is much more useful and informative to cast the expressions in terms of an expansion of the energy 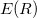$E(R)$ in powers of displacements

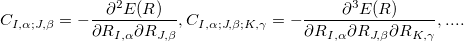$\begin{equation} \label{fc} C_{I,\alpha ;J,\beta } = -\frac{\partial ^2{E(R)}}{\partial R_{I,\alpha } \partial R_{J,\beta }}, C_{I,\alpha ;J,\beta ;K,\gamma } = -\frac{\partial ^3{E(R)}}{\partial R_{I,\alpha } \partial R_{J,\beta } \partial R_{K,\gamma }},.... \end{equation}$

(56)

where Greek subscripts 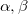$\alpha , \beta$ ,..., denote Cartesian components.

Within harmonic approximation, the vibrational modes at frequency $\omega$ are described by displacements

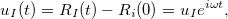$\begin{equation} \label{wave} u_ I(t) = R_ I(t)-R_ i(0)=u_ Ie^{i\omega t}, \end{equation}$

(57)

so that equation 55 becomes:

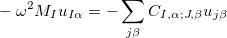$\begin{equation} \label{wave} -\omega ^2 M_ I u_{I\alpha } = -\sum _{j\beta } C_{I,\alpha ;J,\beta } u_{j\beta } \end{equation}$

(58)

the solution of the equation is the set of independent oscillators, each with vibrational frequency $\omega$ ,

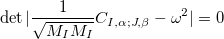$\begin{equation} \label{wave} \det |\frac{1}{\sqrt {M_ I M_ I}} C_{I,\alpha ;J,\beta } - \omega ^2|=0 \end{equation}$

(59)

In a crystal, the atomic displacement eigenvectors obey the Bloch theorem, i.e., the vibrations are classified by k with the displacement. Therefore, the vibrations can be reduced to the first BZ. For a unit cell with N atoms, the phonons at different k yield dispersion curves, which are solution of the 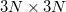$3N \times 3N$ determinant equation:

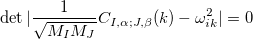$\begin{equation} \label{eq:fc} \det |\frac{1}{\sqrt {M_ I M_ J}} C_{I,\alpha ;J,\beta }(k) - \omega ^2_{ik}|=0 \end{equation}$

(60)

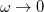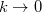There are three acoustic modes with $\omega \rightarrow 0$ for $k \rightarrow 0$ and the other 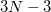$3N-3$ modes are classified as opitc.