-
The relativistic Doppler effect
for
EMR
in vacuum
is
significantly different than the
classical (or nonrelativistic) Doppler effect for
mechanical waves
(i.e., waves in
a medium).
The classical Doppler effect
for mechanical waves
and its formulae
are derived and somewhat explicated in
Waves file:
doppler_effect_classical_derivation.html.
- Why the significant difference? Most importantly EMR (in vacuum) is actually intrinsically in the extreme relativistic limit since it travels at the invariant vacuum light speed c = 2.99792458*10**8 m/s (exact by definition) ≅ 3*10**8 m/s = 3*10**5 km/s ≅ 1 ft/ns for all inertial-frame observers.
So phase velocity is the invariant for all observers (no matter how they are moving) unlike the classical Doppler effect for mechanical waves where the invariant for all observers is wavelength. Note we will NOT expand on the weird effects of special relativity here.
The upshot of the foregoing is that the behavior and formulae are different for the relativistic Doppler effect for EMR from those for the classical Doppler effect.
If you consider EMR in a medium, you have to deal both with frame-dependent phase velocity and relativistic effects.
But we will avoid this tricky case.
Note air is approximately a vacuum for most purposes.
- Qualitatively, the Doppler effect is the same for EMR as it is for mechanical waves in a key respect.
If you move in the wave propagation direction, the frequency decreases (i.e., there is a redshift). If you move opposite the wave propagation direction, the frequency increases (i.e., there is a blueshift).
The Doppler shifts are illustrated in the image.
If you move perpendicular to the wave propagation direction, there is a relativistic Doppler effect the transverse Doppler effect, but it is very small usually and we will NOT consider it further.
- However, there are key differences.
We only explicate them here for motion along or opposite the wave propagation direction for simplicity.
First, for the classical Doppler effect for mechanical waves, except to 1st order in small observer velocities, the Doppler shift in frequency between two observers depends on their individual velocities. But for relativistic Doppler effect (in vacuum), it depends on (and only on) the relative velocity between the two observers.
Second, for the classical Doppler effect for mechanical waves, the Doppler shift in wavelength depends only on source velocity relative to the medium. But for relativistic Doppler effect (in vacuum), it depends again on (and only on) the relative velocity between any two observers (one of whom may also be a source).
In fact, the relativistic Doppler effect (in vacuum) is simpler to understand given the vacuum EMR phase velocity formula fλ=c: any increase/decrease in frequency correponds to an inverse decrease/increase in wavelength. So, in fact, one does NOT need to always refer to both frequency and wavelength Doppler shifts since one kind of Doppler shift implies the other. This is NOT true for the classical Doppler effect.
- In astronomy for EMR, it is conventional to call a Doppler shift---or any kind of wavelength shift---that increases wavelength a redshift because red is at the long wavelength end of the visible band (fiducial range 0.4--0.7 μm).
A Doppler shift---or any other kind of wavelength shift---that decreases wavelength is called a blueshift because blue is at the short wavelength end of the visible band.
The blueshift and redshift astro-jargon is used for all EMR, NOT just visible light.
But why NOT violetshift instead of blueshift? After all, violet is the shortest wavelength visible light.
Probably, because violetshift does NOT trip off the tongue.
Note a blueshift is can be considered a negative redshift and often is in astronomy.
- We will present, but NOT derive, the relativistic Doppler effect formulae for EMR.
The formula for frequency formula is derived from the wavelength shift formula using the phase velocity formula fλ=c. It is
f_2 = f_1 * sqrt[(1-v/c)/(1+v/c)] ,
where the vacuum light speed c = 2.99792458*10**8 m/s (exact by definition) ≅ 3*10**8 m/s = 3*10**5 km/s ≅ 1 ft/ns, v is the velocity along the line of sight of observer 2 relative to observer 1. Note v is positive/negative for recession/approach.
The wavelength shift formula is derived from the frequency shift formula using the phase velocity formula fλ=c. It is
λ_2 = λ_1 * sqrt[(1+v/c)/(1-v/c)] .
- We can do some examples using wavelength shift formula:
- Say v = c/2.
λ_2 = λ_1 * sqrt[(3/2)/(1/2)] = λ_1 * sqrt(3) ≅ λ_1 * 1.7321 ,
and so the wavelength is increased: this is a redshift. - Say v = -c/2.
λ_2 = λ_1 * sqrt[(1/2)/(3/2)] = λ_1 * sqrt(1/3) ≅ λ_1 * 0.57735 ,
and so the wavelength is decreased: this is a blueshift or a negative redshift.
- There is a simplification of the Doppler effect formulae for low relative velocities.
If |v| << c , then we have the frequency 1st order Doppler effect formula
Δf/f = -v/c
which is exactly analogous to the Doppler effect formula for mechanical waves in the case of low velocities for two observers relative to the phase velocity of the medium.
The corresponding wavelength formula is
Δλ/λ = v/c ,
where Δλ is the change in wavelength and λ is either of the observer 1 wavelength or observer 2 wavelength or an average thereof since their difference is insignificant.
- The classical Doppler effect formulae are derived and somewhat explicated in Waves file: doppler_effect_classical_derivation.html.
- Why the significant difference? Most importantly EMR (in vacuum) is actually intrinsically in the extreme relativistic limit since it travels at the invariant vacuum light speed c = 2.99792458*10**8 m/s (exact by definition) ≅ 3*10**8 m/s = 3*10**5 km/s ≅ 1 ft/ns for all inertial-frame observers.
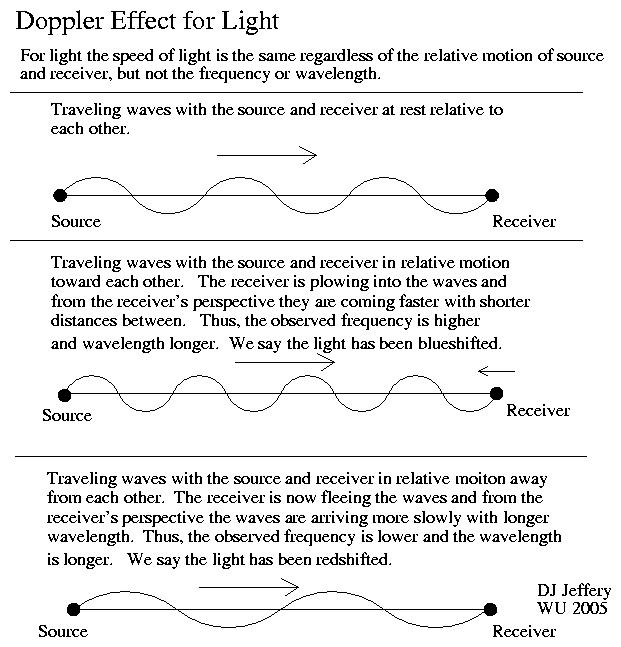
Caption: The Doppler effect for electromagnetic radiation (EMR) in vacuum, where the phase velocity (i.e., velocity of wave propagation) is the invariant vacuum light speed c = 2.99792458*10**8 m/s (exact by definition) ≅ 3*10**8 m/s = 3*10**5 km/s ≅ 1 ft/ns.
For the second panel in the image, instead of "wavelength longer" read "wavelength shorter".
In vacuum, the Doppler effect for EMR is always the (extreme limit) relativistic Doppler effect.
Explication of the Doppler effect for electromagnetic radiation (EMR) in vacuum:
Local file: local link: doppler_effect_relativistic.html.
File: Waves file: doppler_effect_relativistic.html.