First off, if you do want to compact your light collecting area (i.e., light gathering power) and use only one (slightly curved) regular polygon for your segments for simplicity, there are only 3 regular tiling polygons for 2-dimensional Euclidean space (which is approximated by primaries to some degree): equilateral triangles (which we just call triangles hereafter), squares, and regular hexagons (which we just call hexagons hereafter).

1. As you move along a side of a regular polygon (which we just call a polygon hereafter), let the bend angle form one side to the next be θ. Clearly, 2π = nθ, where n is the number of sides. Note n must be an integer ≥ 3.
2. Therefore, θ = 2π/n.
3. If there is a joint vertex of m polygons where they meet without overlaps or gaps between the m polygons (where m must be an integer ≥ 3), then

     2π = m(π-θ) =  m(π-2π/n)
     m = 2/(1-2/n) = n/[(n/2)-1]
       = 6 for n = 3 which is the smallest allowed n,
       = 4 for n = 4,
       = 10/3 for n = 5 which is impossible 
                       since m must be an integer,
       = 3 for n = 6. 

   Note the function m(n) is monotonically decreasing with n and the only stationary point is at n=∞, where m(n=∞)=2.
4. The conclusion of the last item is that it is a necessary condition for regular tiling polygons that n = 3, 4, or 6. But we still have to prove that n = 3, 4, and 6 give regular tiling polygons.
5. If you make m polygons meet at a joint vertex without overlaps or gaps and you go along any joint side from the meeting point, at 1 side length, you come to an opening which is has an angle (m-2)*θ. You can fill that opening with (m-2) more polygons creating a new joint vertex (without overlaps or gaps). You can keep doing this procedure from any new joint vertex covering more of 2-dimensional Euclidean space without end and without overlaps or gaps. Thus, the polygons, you are using are regular tiling polygons and we know that the only polygons we can do this procedure with are those with n = 3, 4, and 6.
6. The last item concludes the proof that there are only 3 regular tiling polygons and they have sides n = 3, 4, and 6: i.e., they are triangles, squares, and hexagons.
7. Actually, you can prove that triangles, squares, and hexagons can tile all 2-dimensional Euclidean space directly:
   1. For squares, create an infinite row of contiguous squares and then pile the rows infinitely and you have tiled all 2-dimensional Euclidean space.
   2. For triangles, create an infinite row of contiguous triangles with alternating orientations and then pile the rows infinitely and you have tiled all 2-dimensional Euclidean space.
   3. For hexagons create an infinite row of contiguous hexagons with a zigzag pattern and then pile the rows infinitely and you have tiled all 2-dimensional Euclidean space.

8. But still why hexagonal segments for segmented mirrors? Why NOT triangles or squares?

   Well, someone knows, but let's try guessing.

   1. It seems most likely to yours truly that hexagons were preferred because they are rounder than triangles and squares, and therefore maybe just a bit easier for active optics to control.

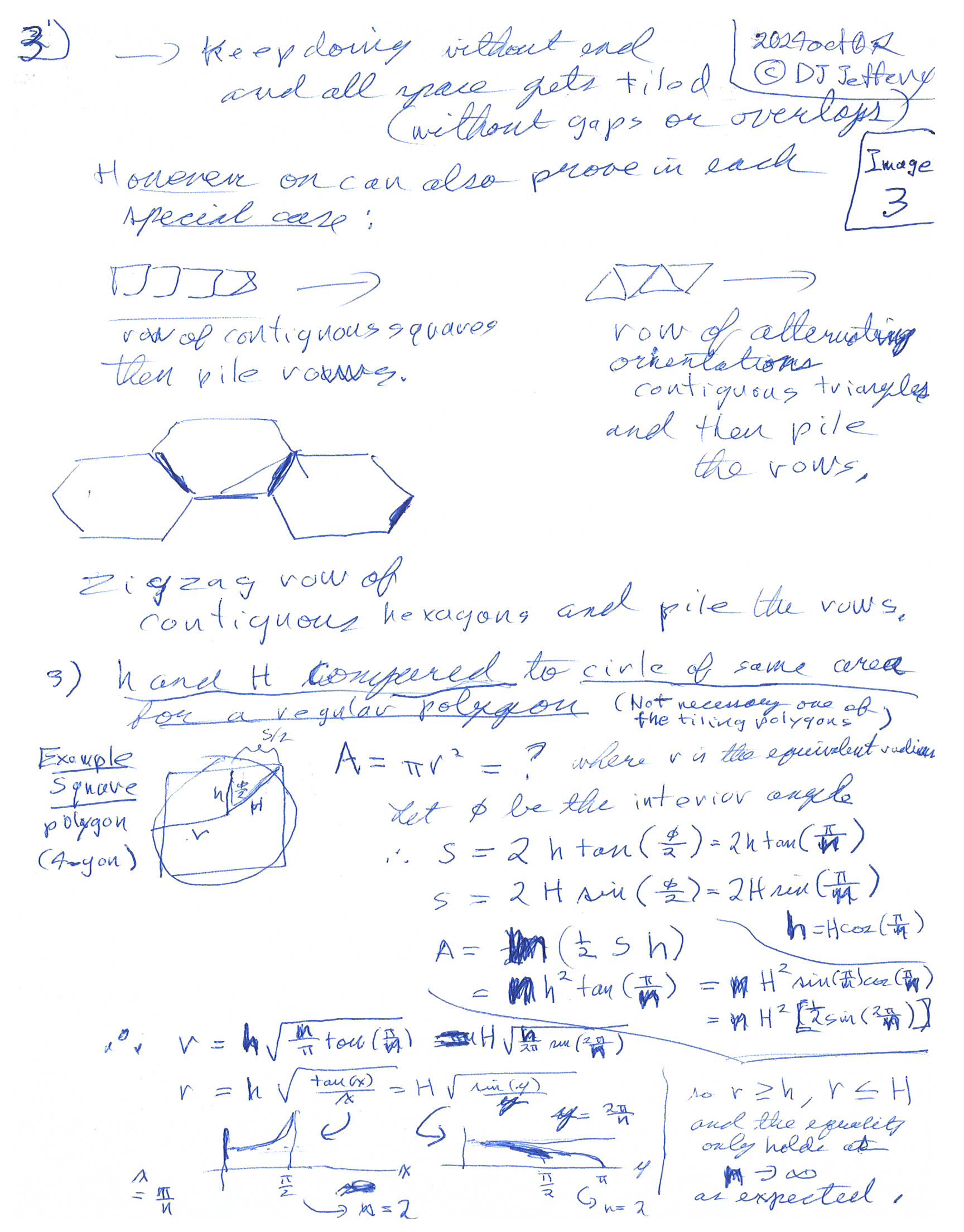
      By rounder, we mean that the mininum/maximum distance (which we call h/H) to a side are as large/small as they can be relative to a radius of circle of the same area as the regular tiling polygons. This statement is proven by the formulae for the such a radius: i.e.,

        r = h*[(tan(x)/x]**(1/2) = H*[(tan(y)/y]**(1/2)  , 

      where x=π/n and y=2π/n. With some insight from Image 3, it should be clear that as n gets bigger, h/H must get bigger/smaller to maintain the equalities in the formulae. In fact, for n→∞, r = h = H since the polygon has become a circle.

   2. Somewhat less likely to yours truly is that the perimeter length of the hexagon relative to that of a circle of the same area as the regular tiling polygons is the smallest. This statement is proven by the formula for the ratio R of the former to the latter: i.e.,

        R = [(tan(x)/x]**(1/2)  ,  

      where x=π/n. With some insight from Image 4, it should be clear that as n gets bigger, R gets smaller. In fact, for n→∞, R = 1 since the polygon has become a circle.

      The upshot is you need less boundary material and/or work on hexagonal segments as compared to triangle and square segments.

      The saving-on-perimeter-length theory seems like a very minor saving to me for making segments, and so probably NOT worth consideration for that. However, the saving-on-perimeter-length theory is one of the theories as to why honeycombs are made of hexagonal cells (Wikipedia: Honeycomb: Geometry; Wikipedia: Honeycomb conjecture, but note the theorem cited here does NOT seem to apply to real honeycombs which do NOT have circular holes). The theory is that honey bees evolved to make them aim to make honeycombs with greatest compactness and minimum material (i.e., to make hexagon cells) or their collective process of building honeycombs evolved to force them to make hexagon cells every time.

   3. Hexagonal segments give NO straight lines for sliding of large pieces of a segmented mirrors. Yours truly CANNOT see how such sliding would be a problem for segmented mirror, but there might other structures where it is a problem.

   4. Hexagonal segments just look so futuristic. Remember, astronomers have to sell a design to the public.

   File: Telescope file: telescope_segmented_mirror_1bb.html.