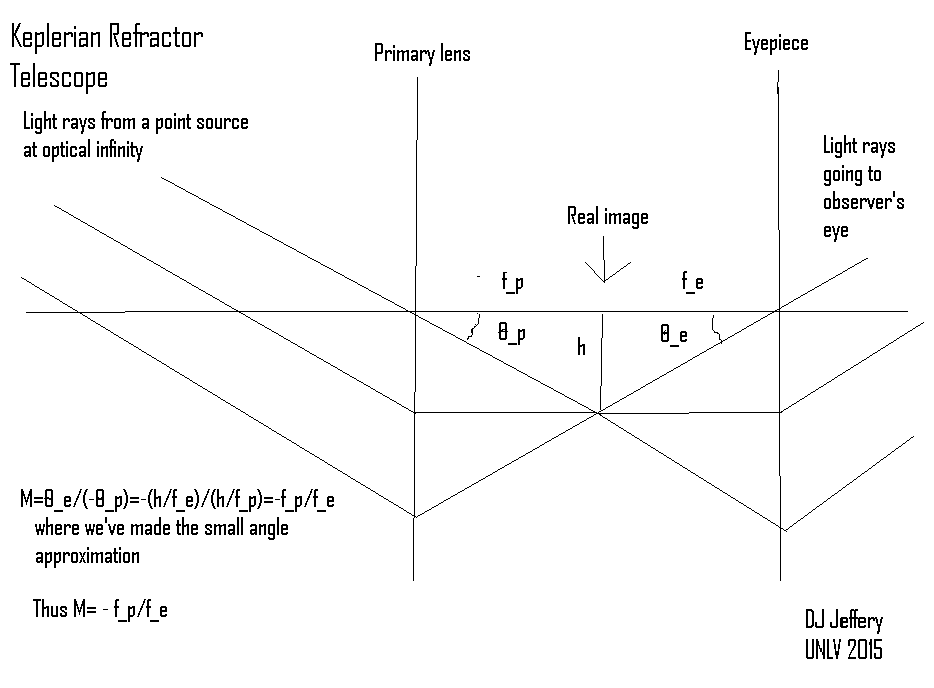
Caption: A diagram of the Keplerian telescope, a classic refractor telescope.
Features:
- A refractor telescope
consists of two
converging lenses
(here represented by vertical lines) aligned along and centered on an
optical axis.
The one to the left is the objective (AKA primary) lens
and the one to the right is the
eyepiece.
- The setup here has the telescope
focused
at optical infinity:
i.e., focused for
point sources of light
so far away that light rays
from them are effectively parallel.
This setup is normal for astronomical observations.
- Our analysis is in the
Gaussian optics limit
of geometrical optics
which itself is one limit
of physical optics.
Gaussian optics assumes the paraxial approximation. This assumption means that light rays make sufficiently small angles to the optical axis that trigonometric functions can always be treated in the small angle approximation.
Geometrical optics itself is the limit of physical optics in which diffraction is neglected and light is treating just as propagating light rays.
- The
primary
forms a real image
at its focal plane
which is at the
focal length f_p along the
optical axis.
Speaking of telescopes in general, the primary is the light-gathering optical device of a telescope AND is usually the first optical device the in the formation of the observed image.
The main parameter (controlling variable) of the primary (and also of the the telescope as a whole) is its diameter. The light-gathering power varies as collecting area of the primary, and thus as the the square of the diameter.
The primary is a mirror for a reflector telescope and a lens for a refractor telescope.
- The real image is the
vertical line downward from the optical axis of length h.
Somewhere off to the left at optical infinity is
the REAL OBJECT which is a vertical line that stands upwards from the
optical axis.
For clarity, we only show a representative set of light rays that form the tip of the real image. The tip is a point real image.
The tip of the REAL OBJECT emits a continuum family of parallel light rays that impact the primary which is the aperture of the telescope.
Light rays that miss the aperture, of course, don't get redirected to help form the tip of the real image.
- The eyepiece
captures
diverging light rays
from the real image
and converts them into
parallel
light rays.
The observer to the right sees these parallel light rays from the real image, and thus his/her human eye sees the real image at optical infinity.
- The telescope magnification
of the Keplerian telescope
follows from simple geometry
and trigonometry with the
small angle approximation for
the tangent function.
The derivation is given in the diagram itself.
The formula for telescope magnification is M = -f_p/f_e .
- Since magnification
is a ratio of like quantities,
it can be regarded as a dimensionless number: i.e.,
a number that has no units.
But there is a sort of conventional unit: the magnification unit X. The unit X which means "multiplies the angular object by X" or the like. So magnification 10 X means magnification by a factor of 10.
- A few comments about the
telescope magnification M:
- There are several different kinds of
optical magnification.
- Telescope magnification
is an angular
optical magnification:
the angular size of an object is magnified by a factor M to become the final image size that
the observer sees.
- We have derived the
telescope magnification formula for
a Keplerian telescope,
but the formula is general, in fact, as long as the meaning of
f_p is generalized to effective
primary
focal length.
- Clearly from the diagram, M increases linearly with
primary
focal length f_p since the
real image increases linearly with f_p.
The primary focal length is usually a fixed parameter of telescope, and so usually cannot be changed for a given telescope.
- The telescope magnification
increases as 1 over (i.e., is inverse linearly with) the
eyepiece
focal length because the
angular size of the real image
seen in the eyepiece
increases this way.
- Eyepieces
can easily be changed on most telescopes,
and so changing eyepieces is
the main way of changing
telescope magnification
for a given telescope.
Nota bene: the smaller the eyepiece focal length (conventionally given in millimeters), the greater the telescope magnification.
Smaller focal length means the eyepiece has greater converging power.
- The diagram makes clear some of the
limits on telescope magnification.
If eyepiece focal length f_e becomes too small, θ_e (the angular size of the real image) get so large that the tip of the real image will effectively disappear out of the field of view (FOV). You probably can still see something looking at a high angle from the optical axis, but this is not a good observation posture.
In fact, the effective FOV decreases as f_e decreases (i.e., as telescope magnification increases).
Also in fact, if θ_e becomes so large that Gaussian optics fails, then our analysis fails.
- The FOV is also limited
by the fact that if the angular size of the real image
gets too large, the light rays
that form it will hit the telescope tube (not shown).
- The minus sign in the
telescope magnification formula
( M = -f_p/f_e )
indicates that the final image seen by the observer is
point inverted
(i.e., rotated by 180°) from what is seen on the
sky.
The diagram just shows the real image gets flipped. However, the diagram is just a cross-sectional view of a physical system with rotational symmetry about the optical axis. Therefore, the diagrammatic flip implies point inversion.
The minus sign can be suppressed if the point inversion is taken as understood.
- There are several different kinds of
optical magnification.
- And that concludes our story of the
Keplerian telescope.
Image link: Itself.
Local file: local link: telescope_keplerian.html.
File: Telescope file: telescope_keplerian.html.