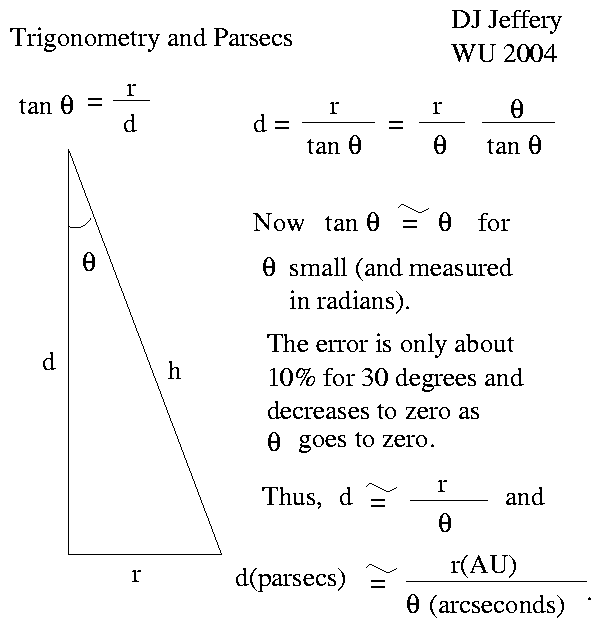
Caption: Trigonometry, parallax, and parsecs illustrated.
From the trigonometry shown in the diagram, we get the stellar parallax formula

Caption: Trigonometry, parallax, and parsecs illustrated.
From the trigonometry shown in the diagram, we get the stellar parallax formula
r(AU)
d(parsecs) = _____________ ,
θ(arcseconds)
where
θ
is the observed parallax
measured in the unit the
arcsecond ('') = 1/3600°,
r is the baseline distance
measured in the unit the
astronomical unit (AU) = 1.49597870700*10**11 m (exact),
d is the distance to be determined in the
unit the
parsec (pc) = 648000/π AU (exact),
and
the formula
is a
small-angle approximation
formula
that is valid for the specified units.
Note:
1 parsec = 648000/π AU = 206264.806 ... AU = (3.085 677 581 491 367 ...)*10**16 m = 3.261563777 ... lyr ≅ 3.26 lyr ≅ 3 lyr(see Wikipedia: parsec (pc) = 648000/π AU (exact); Wikipedia: astronomical unit (AU) = 1.49597870700*10**11 m (exact), Wikipedia: light-year (ly) = 9.460730472580800*10**15 m (exact)).
Parsecs originally became the distance units of choice in astronomy because they are the distance units the above formula gives:
1 AU / 1 arcsecond = 1 parsec.The parsec is, in fact, a good natural unit for interstellar distances since nearest neighbor stars are typically of order a parsec apart. The light-year is a secondary natural unit for interstellar distances. In fact, the light-year would have been a better choice for the primary natural unit since it gives the lookback time immediately: an astronomical object X light-years away is seen as it was X years ago (more exactly X Julian years ago; the Julian year = 365.25 days exactly by definition). But the dead hand of the past weighs on us.
Credit/Permission: ©
David Jeffery,
2004 / Own work.
Image link: Itself.
Local file: local link: parallax_trigonometry.html.
File: Star file:
parallax_trigonometry.html.