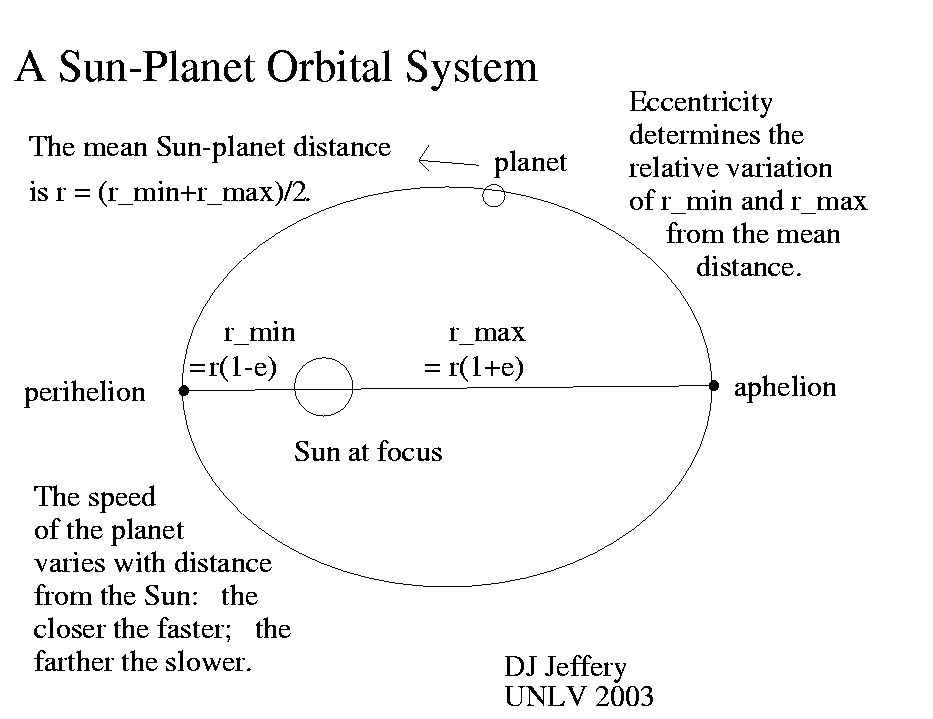
Caption: A cartoon illustrating the Sun and a general (Solar System) planet in an elliptical orbit.

Note that planets orbit the Sun in elliptical orbits to high accuracy/precision is historically speaking Kepler's 1st law of planetary motion.

Features:

1. The Solar System (like most planetary systems) constitutes a very isolated center-of-mass (CM) inertial frame (i.e., inertial frame centered the center of mass of astro-bodies). Thus, the EXTERNAL gravitational field of the rest of the observable universe only affects the center of mass motion and the INTERNAL motions are entirely determined by the INTERNAL gravitational fields and you can neglect the rest of the observable universe in determining them.

2. Note, the formulae for the mean orbital radius (AKA semi-major axis) of a planet and its perihelion and aphelion distances are specified in the cartoon. The "e" is the eccentricity of the elliptical orbit.

   Example planet eccentricities: Venus ♀ e = 0.006772 (smallish), Earth ⊕ e = 0.0167086 (middling), Mars ♂ e = 0.0934 (largish). For all Solar System planet eccentricities, see Solar System file: table_solar_system_planets.html.

3. Now the Sun contains 99.86 % of the Solar System's known mass (Wikipedia: Solar System: Composition), and so the Sun's center is to 1st order at the Solar System center of mass. However, the Solar System center of mass moves around depending on the overall arrangement of Solar System astro-bodies and is only sometimes inside the Sun (see Wikipedia: Heliocentric_orbit).

4. The Sun's mass dominance means that to 1st order the Sun and each planet constitutes just by itself a gravitational two-body system with the Sun sitting unmoving at the center of mass, and thus at one of the focus points of the planet's elliptical orbit.

   This situation is what the cartoon illustrates.

   See the Sun dominator in the figure below (local link / general link: sun_dominator.html).

   ---

5. Of course, the gravitational fields of other planets cause gravitational perturbations on gravitational two-body system of the Sun and a first-specified planet, and so the gravitational two-body system will NOT exhibit an exact elliptical orbit.

   To put the last statement in other words, the gravitational force explicitly obeys Newton's 3rd law of motion: for every force there is an equal (in magnitude) and opposite (in direction) force. However, the Sun's dominance in mass means the sum of the all the planet gravitational forces on the Sun is just a gravitational perturbation.

6. To expand on why the Sun and each planet constitutes its own gravitational two-body system to 1st order, recall Newton's law of universal gravitation for 2 point masses or 2 spherically symmetric bodies:

            G * M_1 * M_2
     F =   ---------------   ,
                r**2 

   where F is size of the pulling gravitational force each object exerts on the other, gravitational constant G=6.67430(15)*10**(-11) (MKS units), (M_1 * M_2) is the product of the object masses, and r is their separation for point masses or their center-to-center separation for spherically symmetric bodies.

   Now solar mass M_☉ = 1.98855*10**30 kg is so much larger than any planet mass that (M_1 * M_2) for Sun and planet is much larger than (M_1 * M_2) for any planet and planet. Thus, the gravitational force between Sun and planet is much larger than for any planet and planet. In fact, the gravitational force between any planet and planet is negligible to 1st order, but NOT to higher order.

7. What if the Sun vanished?

   If the Sun suddenly vanished, the planets would fly away from each other in space and NEVER meet again because the major source of gravity was gone. Yours truly can---if yours truly has the equipment handy---do a demonstration with a swirling object.

   The moons would stay gravitationally bound to the planets, of course.

   If the planets suddenly vanished, the Sun would barely notice.

8. The discussion of this figure is for the Sun and planets. However, the discussion generalizes immediately for almost all single star planetary systems and virtually all planet-moon systems throughout the observable universe. There are complications for multiple-star systems that we will NOT expand on here.