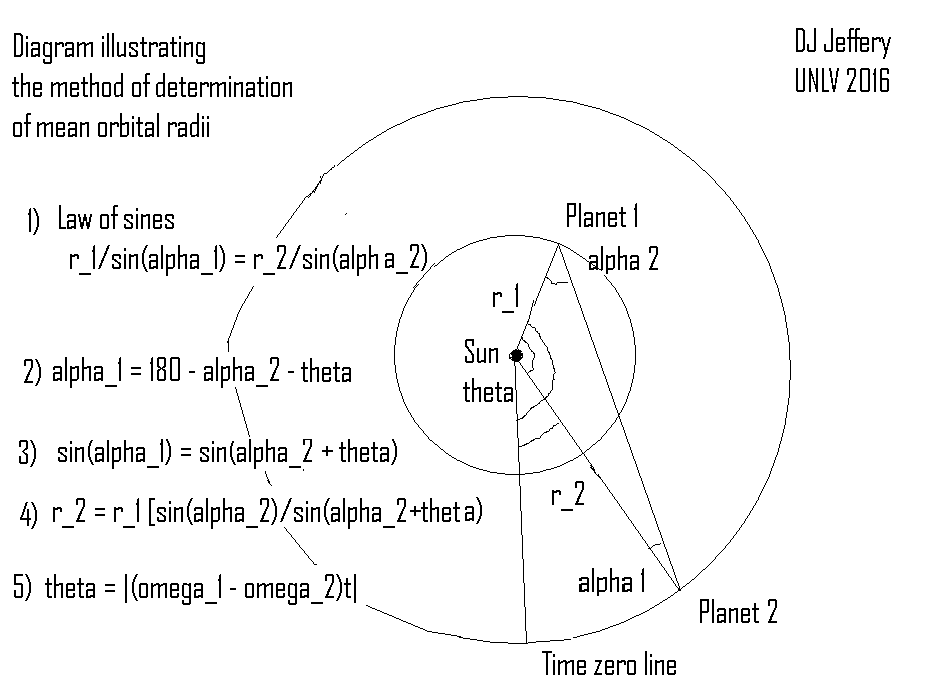
Caption: A diagram illustrating the General Procedure for Orbital Radius Determination for the Solar-System planets in astronomical units (AU) (natural unit for the Solar System) using angular positions measurement for the planets and trigonometry.

We derive this procedure below. The derivation is a bit tedious, but the conceptually easy and using the procedure is cinchy.

Derivation of the General Procedure for Orbital Radius Determination:

1. We derive the general procedure making the simplifying assumptions planets have circular orbits and move at constant angular velocities on their orbits as seen from the Sun---this means they also have constant speeds in space.

2. Consider planet 1 and planet 2 shown in the diagram.

   In the diagram, we have made planet 1 the inner planet and made it counterclockwise from planet 2, but, in fact, the derviation given here is general and either planet can be the inner planet and be counterclockwise of the other.

   We take planet 1 to be the planet of the observer: i.e., to be Earth

3. The mean orbital radius of planet 1 is 1 AU by definition.

   The mean orbital radius of planet 2 is the unknown we are solving for.

4. The planet are shown at time t, where time zero was at inferior conjunction/opposition for an inferior planet/superior planet 2.

5. The sidereal period of planet 1 (i.e., Earth) can be determined directly from the period of the Sun's complete cycle on the ecliptic relative to the fixed stars.

   From the synodic period of planet 2, we can determine its sidereal period (see synodic_period.shtml).

   The synodic period is a direct observable, of course.

6. The angular velocity ω of a planet is then given by ω = 360°/t_p, where t_p is the sidereal period and ω is in degrees per unit time. If one used 2π instead of 360°, the angular velocity would be in radians per unit time.

7. At time t, the angle between the planets subtended at the Sun is θ = |(ω_1 - ω_2)t|.

   Note the ω_i's can be positive or negative and we can let the clock run backward making t negative. However, the absolute value function ensures that θ ≥ 0. For simplicity, we require t sufficiently small that θ < 180°.

   Actually, if 180° ≤ θ ≤ 360°, one just uses 360° - θ instead of θ.

8. From the law of sines (see law_of_sines.html), we have

       r_1/sin(α_1) = r_2/sin(α_2) ,

   where note that α_2 is the elongation of planet 2 and α_1 is the astronomical phase angle of the observed planet 2.

9. Now α_2 is a direct observable.

   And α_1 by the sum-of-angles-of-a-triangle rule is given by α_1 = 180° - α_2 - θ. Now

       sin(α_1) = sin(180° - α_2 - θ) = sin(α_2 + θ) ,

   where the last equality follows from the sine-of-difference formula.

10. Finally, we obtain

        r_2 = r_1*[sin(α_2)/sin(α_2+θ)] ,

    where everything on the right-hand side is a known.

    Thus, we have obtained planet 2's mean orbital radius in terms of known quantities.

    Note if α_1 is 0° or 180°, then α_2 is, respectively, 180° or 0°. In this case, the sines are both 0 and the procedure is indeterminate. Thus, the procedure fails for time zero, but for any time t greater than time zero consistent with our restrictions on θ, it will give the mean orbital radius of planet 2.

    In practice, one would like to chose the situation where the measured/calculated angles give large sines in order to make the relative error small in the calculation.

11. There is simple special case. If planet 2 is an inferior planet, it will reach observable greatest elongations where the line from planet 1 to planet 2 must be tangent to the circular orbit of planet 2, and therefore it follows that at greatest elongations, α_1 = 90°: i.e., it is a right angle. So at greatest elongations, we have r_2 = r_1*sin(α_2) and r_2 can be determined without knowing the angular velocities, and thus without knowing the sidereal periods.

    The corresponding case for a superior planet is quadrature where α_2 = 90°: i.e., it is a right angle. But this is no great help since we still need the angular velocities to find θ.

12. Actually, the procedure requires corrections because the simplifying assumptions are NOT correct: the orbits are NOT exactly circular, the Sun is NOT exactly at the geometric center of the orbits, and the orbital angular velocities are NOT exactly constant. These corrections can be made.

13. Note that the procedure of determining mean orbital radii is based on the heliocentric solar system model.

    The procedure was known to Nicolaus Copernicus (1473--1543) and enabled him to determine mean orbital radii of the planets in astronomical units. He probably did in a much klutzier formulation of the procedure.

    Since heliocentric solar system model predicted the mean orbital radii and the geocentric solar system model did NOT, the heliocentric solar system model was a more powerful theory in respect to giving the structure of the Solar System irregardless whether it was true or not.

    And, of course, the heliocentric solar system model was true.

    It is possible that Aristarchos of Samos (c. 310--c. 230 BCE), who proposed the heliocentric solar system model in Classical Antiquity, was aware of the procedure of determining mean orbital radii. However, nothing in the historical record shows that anyone did before Copernicus.