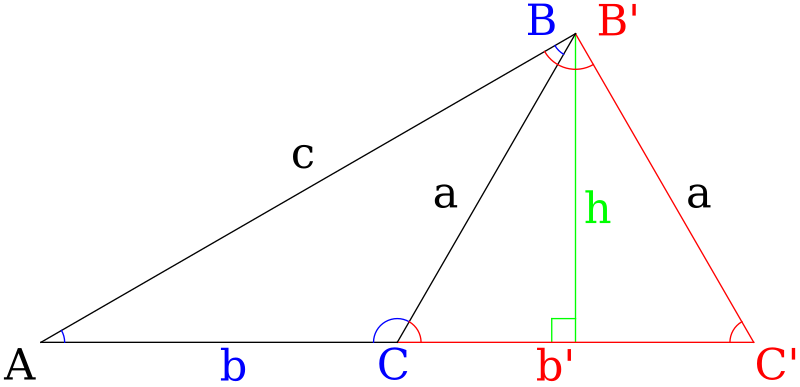
Caption: The proof of the law of sines illustrated.

Proof:

1. Consider the triangle defined by the vertices/angles A, B, C.

   We replace B and C by B' and C' as needed.

   Note that h is a perpendicular dropped from vertex B.

2. From the sine function of trigonometry, we see that:

     c*sin(A) = h = a*sin(180°-C) = a*sin(C) ,

   where we have used the trig identity sin(180°-C) = sin(C).

   We now immediately see that sin(A)/a = sin(C)/c.

3. The same result follows if the perpendicular is inside the triangle, mutatis mutandis, except that trig identity sin(180°-C) = sin(C) is NOT needed. The diagram illustrates this case with the triangle defined by the vertices/angles A, B', C'.

4. The result sin(A)/a = sin(C)/c is now proven in general.

5. Now note that vertices/angles A and C are general. It follows that the result extends to vertex/angle B, mutatis mutandis.

   Thus, we arrive at the final result

     sin(A)    sin(B)     sin(C)
    ------- = -------- = -------  which is the law of sines, QED.
       a         b          c 

1. If for a triangle you are given a side and 2 angles, the triangle can be completely solved for. The third angle follows from the triangle-angles-sum-to-180° rule. The other sides follow from the law of sines.

2. If for a triangle you are given 2 sides adjacent to a given angle, then the law of cosines allows to find the third side. Using the law of cosines again, you can find a second angle and the third angle then follows from the triangle-angles-sum-to-180° rule.

3. If for a triangle you are given 2 sides and one angle which is NOT adjacent to one of the sides, the triangle may or may not be completely solved for.

   There are 2 possible solutions. This arises from the fact the law of sines gives the sine of an angle, not the angle itself.

   1. Say you were given A, a, and c as in the diagram. The law of sines would then give you sin(C) or sin(C'=180°-C) which are equal according to the trig identity sin(180°-C) = sin(C). Which angle C or C' is the solution that applies to the triangle?

      Well both are allowed solutions if they satisfy the triangle-angles-sum-to-180° rule: i.e., A + C < 180° and A + C' = A + (180°-C) < 180°.

      If both these inequalities hold, then both solutions lead to a triangle. Then B = 180°-A-C < 180° and B' = 180°-A-C' < 180° and then sin(B or B') is valid and then side b or b' can determined from the law of sines.

      If the problem is specified has having only one solution, then more information is needed to determine which of the possible solutions is that one solution.

   2. If one of A + C < 180° and A + C' = A + (180°-C) < 180° does NOT hold, then the other must and leads to a unique solution for the triangle.

   3. Note that if you add A + C < 180° and A + (180°-C) < 180°, you get A < 90° which is a weaker condition than the 2 original ones.

      If A < 90° holds, there may be 2 solutions, but there may still be a unique solution. For example, say that A = 80°, C = 5°, and C' = (180° - 5°) = 175°. In this case, B = 180° - 80° - 5° = 95° for a solution, but B' = 180° - 80° - 175° = -75° does NOT give a solution.

      However, if A < 90° is violated (i.e., A ≥ 90°), then one or both of A + C < 180° and A + (180°-C) < 180° is violated and there can only be a unique solution or NO solution (e.g., with A = 179° and C = 5°).

Credit/Permission: © User:Ant.ton.t, 2013 / CC BY-SA 3.0.
Image link: Wikimedia Commons.
File: Trigonometry file: law_of_sines.html.