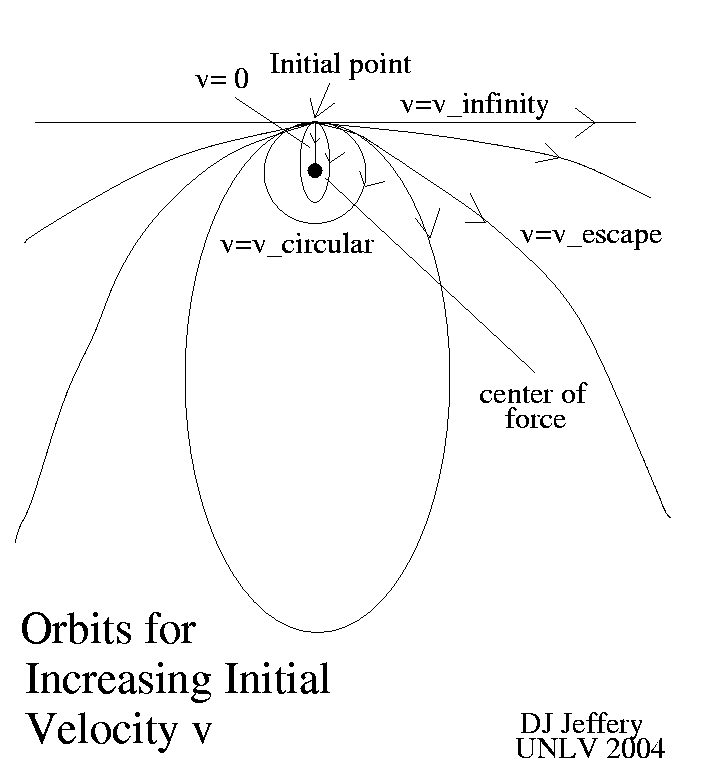
Caption: The orbit for a test particle (i.e., an object of negligible mass) launched near a gravitational center of force as launch initial-condition velocity v is increased from 0 to ∞.

The launch is perpendicular to the line to the center of force at distance R away. These are fixed initial conditions.

No other forces act: e.g., air drag, etc.

The center of force could be an ideal point mass or it could be a finite size spherically symmetric sphere. In the later case, if the test particle hit the center of force, forces other than gravity would act.

The system is analogous to Newton's cannonball thought experiment (or Gedanken experiment).

Cases as velocity v is increased:

1. v = 0 gives eccentricity e = 1 and the test particle falls directly to the center of force.
2. v ∈ (0,v_circular) gives an elliptical orbit with e ∈ (0,1), with the e DECREASING as v increases, and the test particle starts at apoapsis: i.e., the center of force is at the far ellipse focus.
3. v = v_circular gives a circular orbit with e = 0, uniform circular motion, and the center of force is at the center of the orbit. See the circular orbit velocity formula below.
4. v ∈ (v_circular,v_escape) gives an elliptical orbit with e ∈ (0,1), with the e INCREASING as v increases, and the test particle starts at periapsis: i.e., the center of force is at the near ellipse focus.
5. v = v_escape gives an escape orbit with e = 1 and a parabolic trajectory. An escape orbit takes anobject to infinity. Escape is to infinity in this context means that the escaping object will NOT come back to the vicinity of the source of gravity, unless another interaction causes a return. Formally, the escaping object will reach infinity only after infinite time. Escape velocity is the minimum velocity needed to escape to infinity from the gravity of an astro-body. At infinity the escaping object will have zero velocity. The simplest case is when the astro-body is spherically symmetric and one neglects complications like air drag, etc. See the simplest-case escape velocity formula given below.
6. v > v_escape gives an escape orbit with e > 1 and a hyperbolic trajectory.
7. v = ∞ gives an escape orbit with e = ∞ and a straight line trajectory.