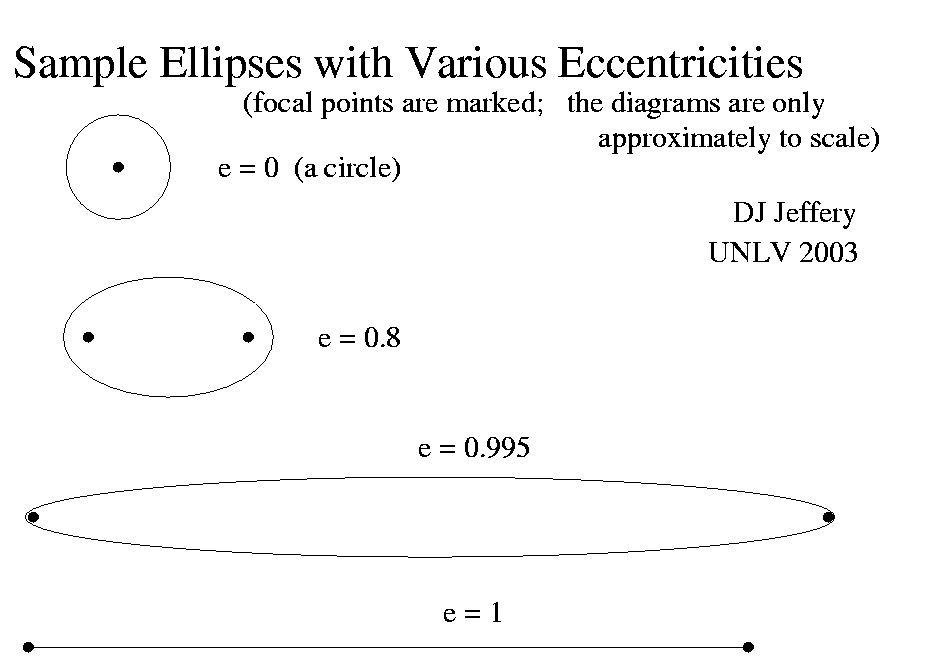

Caption: Two diagrams illustrating how the elongation of an ellipse and the location of its 2 focuses depend on eccentricity e. The second diagram is just an elaboration of the first one.
Features:
- An ellipse
is a plane curve
and, if you neglect scale,
a geometric shape.
- The standard ellipse
formula in
Cartesian coordinates is
(x/a)**2 +(y/b)**2 = 1 ,
"a" is the semi-major axes, "b" is the semi-minor axis, and a ≥ b without loss of generality since one can just flip the names if a < b.If a = b, then the ellipse specializes to the circle with radius a = b.
- The two focuses of
an ellipse have special geometric
significance.
Most obviously, a triangle
with vertices
at the focuses
and on the ellipse curve
has the two sides touching the
ellipse curve
having summed length = 2a
(see Wikipedia:
Ellipse: Definition of an ellipse as locus of points).
- In Newtonian physics,
a bound
2-body system
interacting through a
inverse-square law
force
(e.g.,
a
gravitationally bound
2-body system)
has the 2 bodies
orbiting
their mutual center of mass
in ellipses
with the center of mass
being at a focus
of each
elliptical orbit.
The other focuses
being just empty points in space.
For a gravitationally bound 2-body system as the mass of body_1 (i.e., M_1) goes to infinity relative to the mass of body_2 (i.e., M_2), body_1 goes to being centered on the center of mass. Thus, body_2 effectively orbits body_1 in an elliptical orbit when M_1 >> M_2.
The extreme mass disparity situation is pretty common: e.g., (1) a star is usually much more massive than any of its planets, (2) a planet is often much more massive than any of its moons.
When the extreme mass disparity situation holds between a massive body (usually called the primary) and a group of less massive bodies, then usually to 1st order approximation the massive body and each less massive body from a extreme-mass-disparity 2-body system since the other less massive bodies just cause gravitational perturbations.