
Image 1 Caption: A diagram illustrating the refraction of monochromatic light rays by a prism of made from 5 of the 6 conventional spectral color terms (orange is omitted). The black line segments are normals (i.e., the perpendiculars) to the glass medium interface.
Features:
- Monochromatic light
is an ideal limit that CANNOT be reached in practice.
By monochromatic light,
one means
either an ideal limit
of single wavelength
light or
polychromatic light
with a very
narrow wavelength band.
- The 6 conventional
spectral color terms are:
- violet (fiducial range 0.380--0.450 μm).
- blue (fiducial range 0.450--0.495 μm).
- green (fiducial range 0.495--0.570 μm).
- yellow (fiducial range 0.570--0.590 μm).
- orange (fiducial range 0.590--0.620 μm).
- red (fiducial range 0.620--0.740 μm).
- The light rays
in Image 1
have already been dispersed,
but if you imagine them as
superimposed, they
would be dispersed
by the prism
and the light rays would
be heading in different directions.
Far from the prism
(i.e., in the far field limit), the
light rays would be well
separated into
a continuous spectrum
created by dispersion
by the prism.
- Prisms
disperse
light using
refraction which
is governed by
Snell's law
(AKA the law of refraction).
In many scientific applications,
greater and better
dispersion
is obtained using a
diffraction grating
(which relies on
diffraction rather than
refraction)
rather than a prism.
A compact disc is
incidentally
acts as a crude
diffraction grating.
That is NOT its function, but it
disperses
light rather prettily.
By the by, nowadays
the compact disc
is a retro
technology
(Wikipedia: Compact disc:
Current_status).
For more on compact discs, see
Optics file:
diffraction_compact_disk.html.
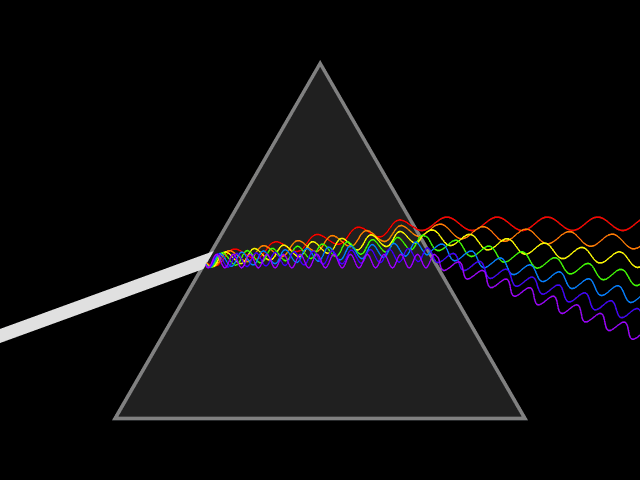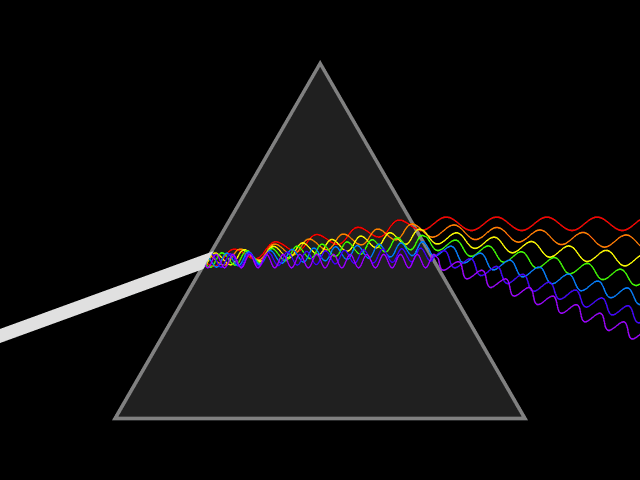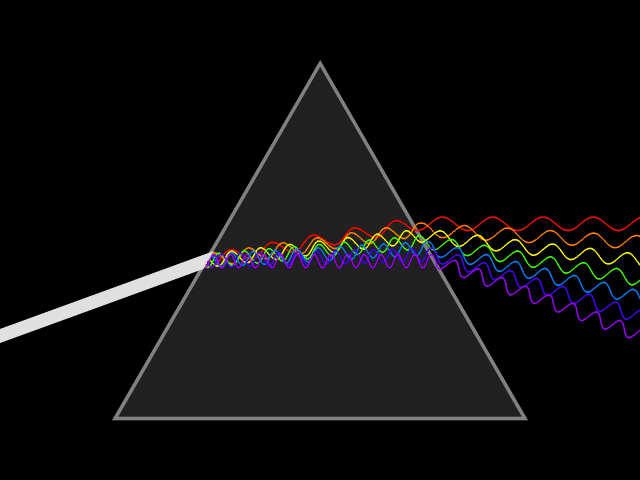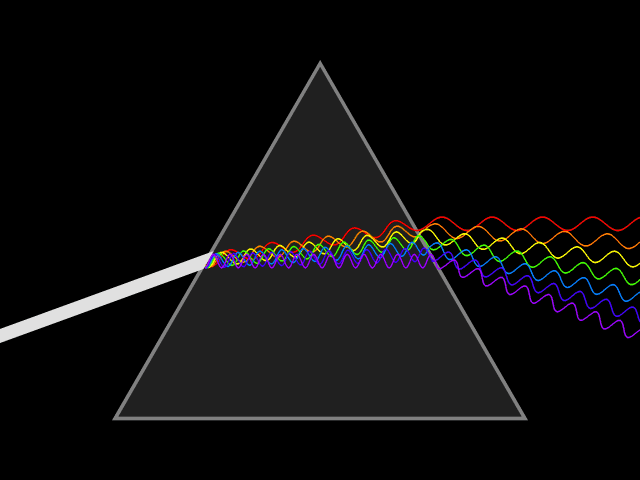
- Image 2 Caption: An animation of how a prism disperses a white light light ray into a continuous spectrum.
In the far field limit, the dispersed continuous spectrum will be well spread out.
- Actually, the prism disperses light beyond the visible band (fiducial range 0.4--0.7 μm) (i.e., into the ultraviolet band (fiducial range 0.01--0.4 μm) and infrared band (fiducial range 0.7 μm -- 0.1 cm)), but the human eye does NOT notice that. For example, a prism made of fused quartz (AKA quartz glass, silica glass) disperses light beyond the visible band (fiducial range 0.4--0.7 μm). Note for fused quartz (AKA quartz glass, the best transmittance range is 0.18--2.7 μm (Wikipedia: Fused quartz: List of physical properties).
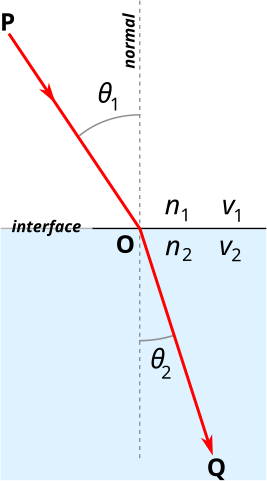
- Image 3 Caption: An illustration of Snell's law (AKA the law of refraction) with refractive index n_2 > n_1. The explication of Snell's law is given below.
- Snell's law (AKA the law of refraction) is
n_1*sin(θ_1) = n_2*sin(θ_2) ,
where the n_i are the refractive indexes n_i = c/v_i (n_i ≥ 1 always), vacuum light speed c = 2.99792458*10**8 m/s (exact by definition) ≅ 3*10**8 m/s = 3*10**5 km/s ≅ 1 ft/ns, v_i is the light speed in optical medium i (v_i ≤ c always), and the θ_i are the angles (i.e., incidence angle and refraction angle) of the light ray from the normal (i.e., the perpendicular) to the medium interface.Note
sin(θ_2) = (n_1/n_2)*sin(θ_1) ,
and so θ_2 subceeds/exceeds θ_1 if n_2 is greater/lesser than n_1.In particular, note that a light ray bends toward a normal going from medium 1 to 2 if n_2 is greater than n_1.
Most common transparent solids and liquids have n_i greater than air's n_air, and so light rays bend toward/away the normal when entering/leaving these common materials when they are embedded in air.
Note incidence angles and refraction angles greater than 90° do NOT happen definitionally and have NO meaning in Snell's law. But what happens for case of incidence angles greater than those that give refraction angles of 90°? Total internal reflection which is illustrated by Image 5 below and which we discuss below Image 5.
- Refractive indexes are generally wavelength dependent. In particular, common transparent solids and liquids have refractive indexes that are noticeably wavelength dependent.
For prisms (which are made from some kind of optical glass), the refractive index decreases with increasing wavelength. Thus, in Image 1 and Image 2, violet light refracts more than the red light.
- How does a prism's work?
Image 1 and Image 2 actually tell all. But we can supplement the images with some description:
- A single polychromatic
incident light ray
(and therefore
an incident
light ray of mixed
wavelengths/frequencies)
on the
prism's
surface at a nonzero
incidence angle
undergoes dispersion
into continuum
colored
light rays
at a
continuum of
refraction angles
inside the prism
because of the
wavelength dependence
of the refractive index.
- Since the
optical glass
has a higher
refractive index
than air,
the refracted
light rays
are bent toward the normal.
- Because of the angling of the
prism's
medium interfaces,
the already dispersed
colored
light rays
are further
dispersed
when they exit the prism.
So there will be a
dispersed
spectrum.
- Note on exiting, the refracted
colored
light rays
are bent away from the normal,
but the aforesaid angling now gives an increase in
dispersion.
- What if a continuum
of polychromatic
light rays
(i.e., a light beam)
were incident on the
prism?
Exiting the prism at short range there is a strong remixing the of the colored light rays, and so the overall emergent light beam will be polychromatic though with a complexly different mixture than the incident light beam.
However, at long range from the prism, the dispersed colored light beams will spread out because they emerge at different angles. So again there will be dispersed spectrum.
- What if the sides of an optical medium object on which there are incident light rays are parallel? For an answer, consider Image 4 and its explication below
By the by, an common example of such an optical medium object is plate glass.

- Image 4 Caption: A monochromatic light ray (maybe produced by a yellow laser, but maybe just well-collimated yellow light ray) being refracted twice by a plastic slab. Overlay description:
- First incidence angle and second refraction angle = α.
- First refraction angle and second incidence angle = β.
- Slab thickness = d.
- As Image 4 shows, if the sides of the slab are parallel, the twice refracted monochromatic light ray is displaced, but its direction is NOT changed.
Note:
- If a
polychromatic
light ray
was used,
the
light ray
would be
dispersed
into a set of
parallel
colored
light rays
propagating in the same direction as the
incident light ray.
- What if a continuum
of polychromatic
light rays
(i.e., a light beam)
were incident on the slab?
Exiting the slab, the colored light rays would be remixed and the exiting light beam would be polychromatic.
- In the case where an incident light beam
was homogeneous and a slab sufficiently long,
the exiting light beam
would have the same
polychromatic
nature as the incident
light beam.
This case is actually what one usually gets with
plate glass.
- The lenses
of eyeglasses do
NOT have
parallel sides.
Thus, there should be some
differential refraction
for polychromatic
light beams (which effect
in the special case of focusing
for lenses
is called
chromatic aberration).
Eyeglass
wearers will thus often see a bit of
dispersion
for light beams incident
on their lenses
are large angles
from the normal.
Typically, the dispersion
occurs for looking at light sources near the edges of the
lenses.
- Image 5 Caption: An illustration showing Snell's law and total internal reflection (with its critical angle θ_critical). Total internal reflection is when a light beam in one optical medium undergoes a reflection at a medium interface with NO refraction into a second optical medium which is, in fact, intrinsically transparent. Total internal reflection happens when the incident incidence angle of a light ray exceeds the critical angle θ_critical for total internal reflection. Total internal reflection is often used in optical devices. For example, see Optics file: optics_prism_porro_double.html.
A derivation of total internal reflection is beyond our scope, but a derivation of the formula for the critical angle θ_critical is given below.
- A light ray from a optical medium 1 CANNOT propagate into a optical medium 2 if the refraction angle is greater than 90° since then it is NOT going into optical medium 2 at all. However, the refraction angle can be as large a 90° and this is the largest it can be. The incidence angle that gives refraction angle 90° turns out to be the critical angle θ_critical for total internal reflection---which is something we CANNOT prove, but we can derive the formula for the critical angle θ_critical from Snell's law
n_1*sin(θ_1) = n_2*sin(θ_2) .
Say θ_2 = 90°, then sin(θ_2) = 1, θ_critical = θ_1, and
θ_critical = arcsin(n_2/n_1) .
Since arcsin(x) is undefined for x > 1, there is only a critical angle for the case of n_2/n_1 ≤ 1: i.e., for the optical medium 1 having having the higher refractive index than optical medium 2.Total internal reflection occurs in optical medium 1 at the medium interface for θ_1 > θ_critical. Total internal reflection is, in fact, specular reflection (if the medium interface is sufficiently smooth) where reflection angle equals the incidence angle as illustrated in Image 5.
- Image 2 Caption: An animation of how a prism disperses a white light light ray into a continuous spectrum.
-
Images:
- Credit/Permission:
© User:RJHall,
2005 /
Creative Commons
CC BY-SA 2.0.
Image link: Wikimedia Commons:
File:Refraction varies by frequency.gif.
- Credit/Permission:
Lucas V. Barbosa (AKA User:LucasVB),
2007 /
Public domain.
Image link: Wikipedia: File:Light dispersion conceptual waves.gif.
- Credit/Permission: User:Oleg Alexandrov,
2007 /
Public domain.
Image link: Wikimedia Commons: File:Snells law2.svg.
- Credit/Permission: ©
User:MikeRun,
2019 /
CC BY-SA 4.0.
Image link: Wikimedia Commons: File:Refraction-photo-with-overlay.png.
- Credit/Permission: ©
User:Jfmelero,
User:Gavin R Putland,
2019 /
CC BY-SA 3.0.
Image link: Wikimedia Commons: File:ReflexionTotal en.svg.
File: Optics file: refraction_prism.html.