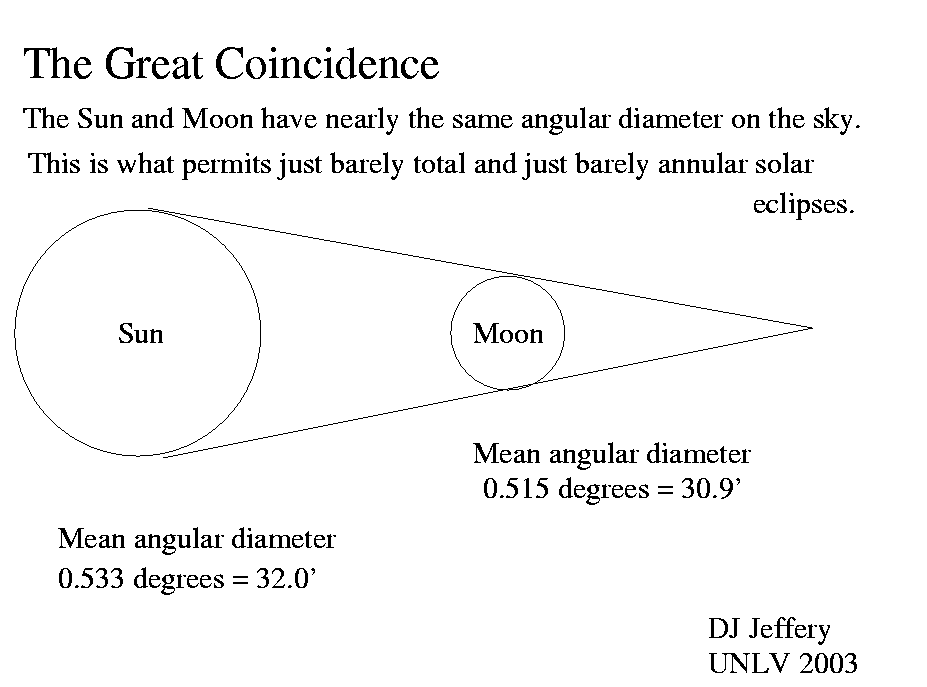
Caption: The great coincidence is near equality of the angular diameters of Sun and Moon as seen on the sky (see EarthSky: Coincidence that sun and moon seem same size? (2013); Wikipedia: Angular diameter: Use in astronomy).

Features:

1. The Sun and the Moon have very different sizes in 3-dimensional space, and so have very different diameters.

2. However, as seen from the Earth, they have approximately the same angular diameter ∼ 0.5°.

   To be precise, as seen from the Earth's center center-to-center distances in the precise calculation of angular diameters ?????, we find:

   1. Sun angular diameter: mean 0.5332°, range 0.5242°--0.5422°.
   2. Moon angular diameter: mean 0.5286°, range 0.4889°--0.5683°. The mean value shown in the image is either somewhat in error or was calculated in a different way from how yours truly now calculates it which is the average of the range limits.

   Of course, we do NOT observe Sun and Moon from the Earth's center, but that is the standard reference observational point and, in fact, the Earth's size is sufficiently small that its size can be treated as negligible in all but highly precise measurments. Recall Earth equatorial radius R_eq_⊕ = 6378.1370 km. Also observing Sun and Moon on the horizon puts them at nearly exactly the same distance as from the Earth's center.

3. Why do we have the great coincidence? Answer: The Sun's diameter is ∼ 400 times the Moon's diameter. But the Sun is ∼ 400 times farther away than the Moon. Thus, the ratio of diameter to distance is approximately the same for both and this means the angular diameter is approximately the same: i.e., ∼ 0.5°.

4. The great coincidence causes there to be just barely total solar eclipses and just barely annular eclipses.

   If the Sun's angular diameter were constant at its mean value, then total solar eclipses would happen (when the Moon is centered on the Sun) when the Moon was slightly closer than its mean distance (i.e., its mean lunar orbital radius = 384399 km = 60.32 Earth equatorial radii = 2.57*10**(-3) AU = 1.282 light-seconds) and the annular eclipses would happen when it was farther. However, since the distance to the Sun (i.e., fiducial value 1 astronomical unit (AU) = 1.49597870700*10**(11) (exact by definition) ≅ 499.00478384 light-seconds ≅ 8.3167463973 light-minutes ≅ 4.8481368111*10**(-6) pc) varies because of the Earth's orbit is elliptical orbit with small eccentricity 0.0167 = 1.67 %, the exact prediction of whether there will be an total solar eclipse or an annular eclipse (when the Moon is centered on the Sun) is complicated. But astrometrists have done that for us in ephemerides.

5. The great coincidence seemed for long ages of human society to have great cosmic significance---a profound symmetry of the two great lights in the sky.

   For example in Greek mythology, the Sun and Moon were viewed as being or as manifesting the twin gods Apollo and Artemis, or, alternatively, just brother-and-sister gods Helios and Selene.

6. But after the rise of modern astronomy, the near equality was seen as the great coincidence, just an accident of Solar System formation and evolution.

   And the great coincidence may indeed be just a coincidence.

   On the other hand, there is now an anthropic principle argument for the great coincidence (see Dynamical, biological, and anthropic consequences of equal lunar and solar angular radii, S. A. Balbus, 2014). Maybe our existence as large terrestrial animals anthropically implies the great coincidence. See file devonian_speciation.html for further discussion of the anthropic principle argument.

   Actually, the argument is only for a near great coincidence. The fact that the Sun and Moon angular diameters are as close as they are still seems to be just a great coincidence.

7. Actually, Earth-Moon distance increases with time and so the Moon angular diameter decreases with time due to tidal acceleration.

   However, this turns out to be a relatively small effect over hundreds of megayears.

   Circa 400 Myr Before Present (BP), the mean mean lunar orbital radius was ∼ 97.7% of its current value and its mean angular diameter was ∼ 0.5410° which is bigger than the current mean Sun angular diameter: (mean 0.5332°, range 0.5242°--0.5422°) and almost as big current maximum Sun angular diameter. (see George E. Williams 2000, Reviews of Geophysics, Volume 38, Issue 1, p. 37-60; Wikipedia: Orbit of the Moon: Tidal evolution of the lunar orbit). Assuming the Sun angular diameter was NOT much different than now total eclipses would have been much more common than now during eclipse seasons and annular eclipses more rare.

   And 50 Gyr in the future, the Moon's angular diameter will only be reduced to ∼ 0.36° assuming the Earth-Moon system is still around. The Earth-Moon system might well have been long vaporized by then in the Sun's post-main-sequence phase which will start ∼ 5 Gyr from now when the Sun expands into red giant star and then an asymptotic giant branch (AGB) star (see Wikipedia: Sun: After core hydrogen exhaustion).