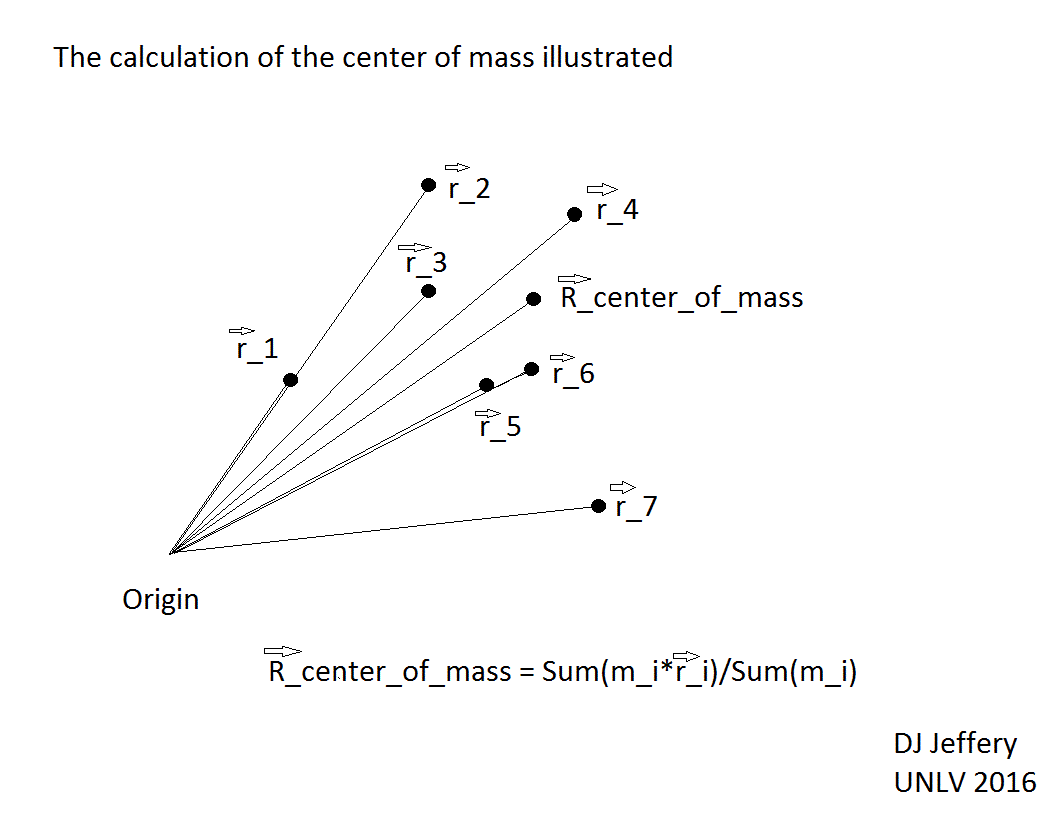
Caption: The calculation of center of mass illustrated.

Features:

1. The center of mass is a mass-weighted average position for a physical system.

2. The system could be anything---fluid body, gas sample, set of point masses, planetary system, star cluster, galaxy, galaxy cluster---anything.

3. You divide the system up mentally into small bits (formally differential elements) and sum position vectors for the bits times the bit masses and divide by the sum of the bit masses (which is the mass of the system).

   The result is the center of mass---more explicitly the center-of-mass position vector.

4. The formula for center of mass is

     R_cm = ∑_i (m_i*R_i) / ∑_i (m_i) = sum;_i (m_i*R_i) / m  

   where capital letters signify vectors, R_cm is the center of mass, i is an index for the bits, R_i is the position vector for bit i, m_i is the mass of bit i, and m is the system mass (i.e., the total mass).

5. The importance of the center of mass of a system is actually the position variable that enters into Newton's 2nd law of motion (AKA F=ma):

     F_net_ext = m*A_cm  , 

   where F_net_ext is the net external force on the system, m is again the system mass, and A_cm is the center-of-mass acceleration.

   So it's center-of-mass motion which is determined by F=ma---a point often neglected in high-school physics courses.

6. Centers of mass are very useful in determining inertial frames for the analysis of both the INTERNAL and center of mass the motions of a system.

   Center-of-mass (CM) inertial frames are discussed in file Mechanics file: frame_basics.html. Their special cases, celestial frames and comoving frames are discussed in file Mechanics file: frame_hierarchy_astro.html.

7. An important factoid is that center of mass of a system equals the center of mass evaluated from the center of masses of any set of subsystems of the physical system.

   Proof:

     m*R_sub_cm = ∑_i ( m_sub_i*R_sub_i ) = ∑_i ∑_j ( m_ij*R_ij ) 
                = ∑_k (m_k*R_k)  = m*R_cm  ,

   and thus vec_R_sub_cm = vec_R_cm,
   

   where "sub" stands for subsystem, R_sub_cm is the center of mass evaluated using the subsystem centers of mass, R_cm is the center of mass evaluated from the elementary particles (i.e., the true center of mass of the system), the index i labels the subsystems, R_sub_i is the center of mass of subsystem i, m_sub_i is the mass of subsystem i, the index ij labels elementary particles in subsytem i (and thus their masses and position vectors), and k labels elementary particles in general (and thus their masses and position vectors). The division into subsystems is general and the division into elementary particles is unique in some mythical limiting sense yours truly hopes.
   QED.