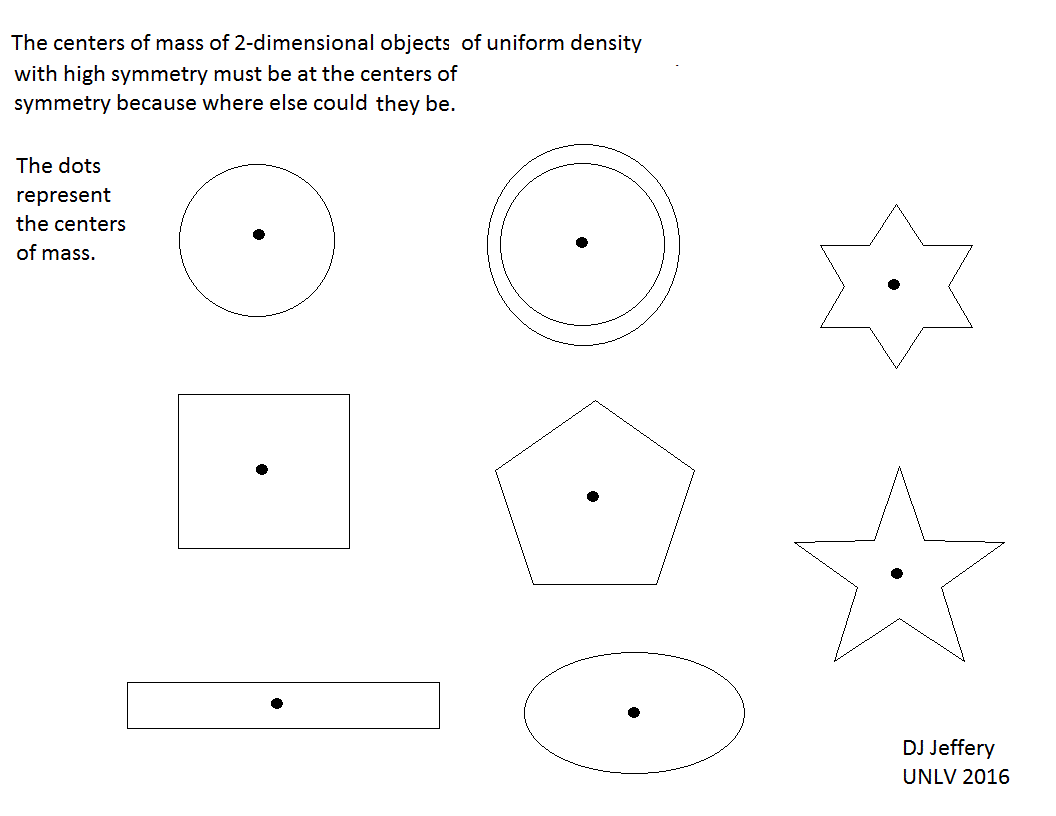
Caption: A diagram illustrating the centers of mass of 2-dimensional objects of uniform density with high symmetry.
Recall, a center of mass is the mass-weighted average position of an object.
You can find these centers of mass of the objects in the diagram by inspection.
Features:
- The centers of mass
of the displayed objects
must be the points
of highest symmetry
(i.e., the centers of symmetry)
because where else could they be if the
symmetry
is NOT to be broken.
The points of highest symmetry are the points about which each object can be rotated into itself by any angle which is multiple of a unit angle specific to the object: e.g., infinitesimal for the circle, 90° for the square, 72° for the regular pentagon and pentagram, etc.
- Many 3-dimensional objects
with simple shapes and uniform
density
also have centers of symmetry
which are also centers of mass
that can be found
by inspection: e.g.,
-
cube,
cylinder,
ellipsoid,
parellelepiped,
Platonic solid,
regular tetrahedron,
sphere,
spheriod (AKA ellipsoid of revolution),
torus,
etc.
- More details about
2-dimensional
objects
of high symmetry and
uniform density
are given in
File: Mechanics file:
center_of_mass_2d_4.html
which may be this file in which case the more details are below.
Credit/Permission: ©
David Jeffery,
2016 / Own work.
Image link: Itself.
Local file: local link: center_of_mass_2d.html.
File: Mechanics file:
center_of_mass_2d_4.html.
File: Mechanics file:
center_of_mass_2d.html.