Parametric equation of an ellispse dynamically illustrated

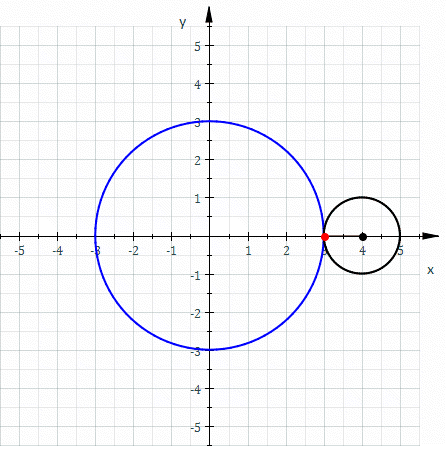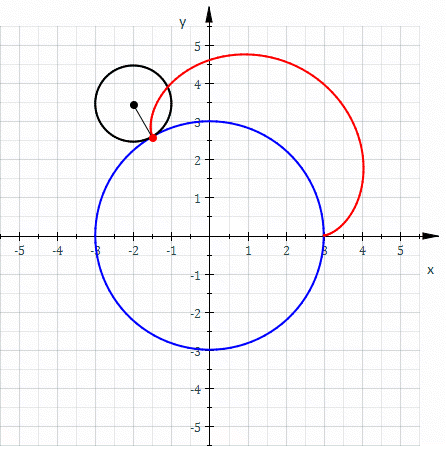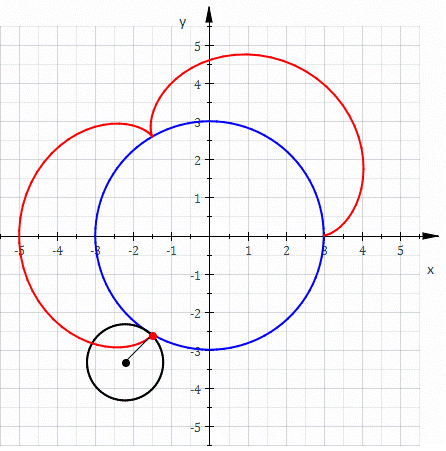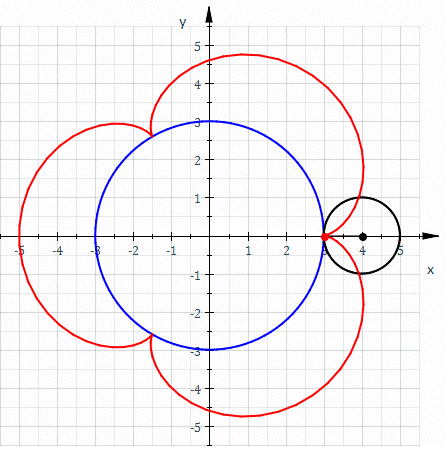
Image 1 Caption: The parametric equation of an ellipse (with center at origin) dynamically illustrated in the animation.

Features:

The blue dot is the point (x,y) on the ellipse being traced out in the complex way illustrated by the blue line which has length equal to the semi-major axis "a" of the ellipse and is directly tracing out a circle. The x component of the vector is clearly
```
  x(t)=a*cos(E)  , 
```
where E is the angle measured counterclockwise from the positive x-axis to the blue line and in astro jargon is called the eccentric anomaly. From the ellipse equation (with "b" being the semi-minor axis), we find:
```
  (x/a)**2+(y/b)**2 = 1  .
  (y/b)**2=1-(x/a)**2 = 1-cos(E)**2 
                      = sin(E)**2
  (y/b) = ± sin(E) where the valid case 
                           is clearly +sin(E)
  y = b*sin(E) 
```
The ordered pair [x(E)=a*cos(E),y(E)=b*sin(E)] constitute the parametric equation of an ellipse. The radius R to the blue dot is
```
  R=sqrt[(a*cos(E))**2+(b*sin(E))**2]  .  
```
Only in the case of a circle where a=b is R=a and the parametric equation reduces to [x(E)=a*cos(E),y(t)=a*sin(E)].
One of the great ironies of the history of astronomy is that ancient authority on ellipses Apollonius of Perga (c.262--c.190 BCE) is believed to have invented epicycle models for planetary orbits instead of using ellipses which are the true shape of planetary orbits to 1st order (see Wikipedia: Deferent and epicycle: History).
Note Apollonius did NOT use formulae in a modern sense. He worked purely in words and diagrams. His understanding of ellipses was based on his study of conic sections which are illustrated in Image 2 and described in the next list item.
Image 2 Caption: "The conic sections (circle, ellipse, parabola, and hyperbola) are 2-dimensional figures formed by the intersection of a plane with a cone at different angles. The theory of these figures was developed extensively by the ancient Greek mathematicians, surviving especially in works such as those of Apollonius of Perga (c.262--c.190 BCE). The conic sections pervade modern mathematics." (Slightly edited.)
Apollonius' "goof" in NOT using ellipses for planetary orbits is explained by noting that the planetary data in his day did NOT compel elliptical orbits and epicycle models seemed adequate and were simpler to understand.
Something always to remember aobut ancient Greek astronomers: they could NOT measure distances to astro-bodies, except that eventually they got a fairly good distance to the Moon of ∼ 60 Earth equatorial radii (with R_eq_⊕ = 6378.1370 km). This meant that could NOT know directly where anything was in 3-dimensional outer space, except for the Moon. For more information on their distance problem, see Ancient Astronomy file: distance_problem.html .
Note in particular that ancient Greek astronomers had difficulty dealing with non-uniform motions which planets have on their elliptical orbits. The ancient Greek astronomers did NOT have calculus which is needed for the mathematical description of non-uniform motions in general.
The approach they took to deal with non-uniform motions in Heavens was decompose them into uniform circular motions that compounded reproduced to some accuracy/precision the motions of the planets.
In Aristotelian cosmology, the uniform circular motions were of compounded celestial spheres that carried the planets around.
In Ptolemaic system, the uniform circular motions were those on the deferent and epicycle of epicycle models.
Compounded uniform circular motions are illustrated in the animation below in Image 3.
Image 3 Caption: An animation where "The red curve is an epicycloid traced as the small circle (radius r = 1) rolls around the outside of the large circle (radius R = 3)." This animation does NOT depict an actual planet epicycle model since there are 3 apparent retrograde motions and actual planet epicycle models had only 1 apparent retrograde motions when in inferior conjunction (for inferior planets) or in opposition (for superior planets).
Before 1600 astronomers working in the western Eurasian tradition of astronomy continued to rely on compounded uniform circular motions in their Solar System models.
The hold of compounded uniform circular motions was only broken by Johannes Kepler (1571--1630) who was one of the leading mathematical innovators of the Scientific Revolution of the 16th and 17th centuries and also a person who was willing to do long tedious calculations to deal with non-uniform motions.
In modern times, epicycles have been used as mathematical tool in analyzing the orbits of astro-bodies in galaxies (see Wikipedia: Lindblad resonance). However, these modern epicycles have been criticized too and maybe are on their way out of modern use (Francis, C. 2011, arXiv:0911.1594v1, "Lindblad's epicycles - valid method or bad science?").

Images:

Credit/Permission: © User:Magister Mathematicae, 2012 (uploaded to Wikimedia Commons by User:Magog the Ogre, 2021) / CC BY-SA 3.0.
Image link: Wikimedia Commons: File:Conic Sections.svg.
Credit/Permission: © User:Sam Derbyshire, 2008 (uploaded to Wikimedia Commons by User:Gengiskanhg, 2021) / CC BY-SA 3.0.
Image link: Wikimedia Commons: File:EpitrochoidOn3-generation.gif.

Local file: local link: ellipse_animation.html.
File: Mathematics file: ellipse_animation.html.