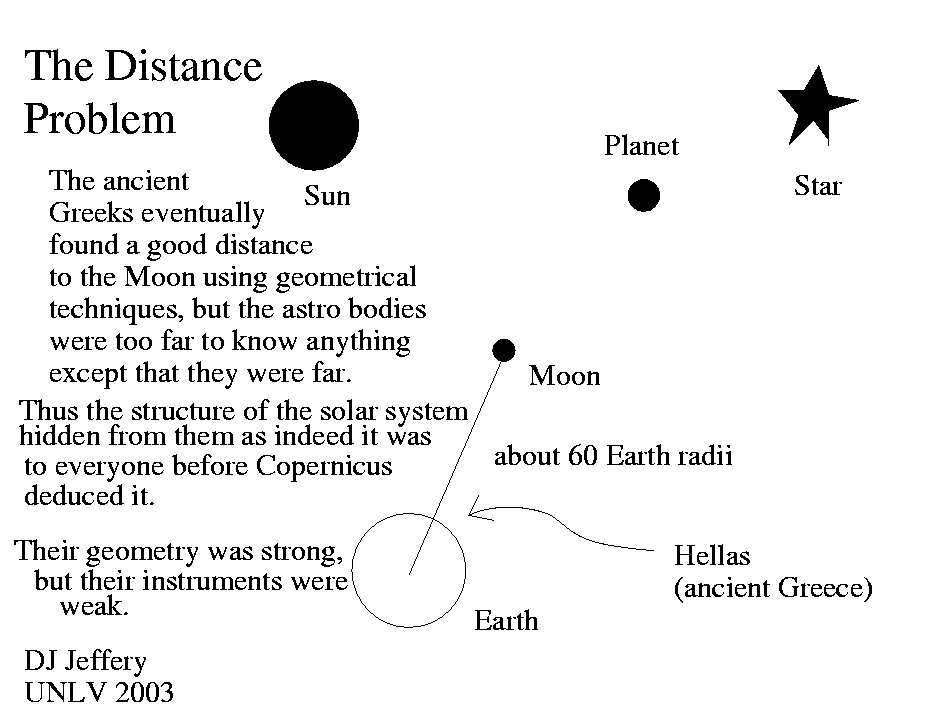
Caption: The distance problem of ancient Greek astronomy and all other ancient astronomies too: They could NOT measure Solar-System distances.

Features:

1. Now the ancient Greek astronomers eventually got a good mean distance to the Moon of ∼ 60 Earth radii. For example, Hipparchus (c.190--c.120 BCE) eventually seems to have obtained a mean distance of 61 Earth radii (Wikipedia: On Sizes and Distances: Conclusion; Wikipedia: Hipparchus: Distance, parallax, size of the Moon and the Sun) and Ptolemy (c.100--c.170 CE) obained a mean distance of 59 Earth radii (Wikipedia: On Sizes and Distances: Book 2 reconstruction (Swerdlow); Wikipedia: Hipparchus: Distance, parallax, size of the Moon and the Sun).

2. The modern accurate/precise values for the mean distance to the Moon are

     R_Moon = 60.2684 R_Earth_eq ≅ R_Earth_eq
            = 2.57*10**(-3) AU
            = 384,399 km ≅ 400,000 km , 

   where R_Earth_eq is the Earth equatorial radius R_eq_⊕ = 6378.1370 km. See also Wikipedia: Lunar distance: Value.

3. But beyond the Moon (which they thought correctly was the closest astro-body), the ancient Greek astronomers' distances were very inaccurate, and so they did NOT know the relative locations of the astro-bodies well enough to understand the Solar System just empirically. Their geometry was strong, their instruments were weak: astrolabe, mural quadrant, etc. (Wikipedia: List of astronomical instruments).

   Actually, the ancient Greek astronomers could have done better with their instruments if they had tried harder like pre-telescopic Ulug Beg (1394--1449) (see Wikipedia: Ulug Beg: Astronomy), Taqi ad-Din (1526--1585), and Tycho Brahe (1546--1601). But also actually, those later astronomers were very well funded. Tycho was funded by Danish King Frederick II (1534--1588; reigned 1559--1588). Taqi ad-Din was funded by Ottoman Sultan Murad III (1546--1595; 1574--1595). Ulug Beg (1394--1449; reigned 1447--1449) was a sultan of the Timurid dynasty---he was a grandson of Timur Lang (1336--1405), AKA Tamerlane Of course, none of Ulug Beg, Taqi ad-Din, and Ulug Beg got distances beyond the Moon either---but they did make better measurements than the ancient Greek astronomers.

4. With NO empircal solution to the distance problem, the ancient Greek astronomers could only measure angular position and make assumptions about distances beyond the Moon if they so chose.

5. What about theoretical distances?

   Almost all ancient Greek astronomers used geocentric solar system models, and so were on the wrong track to getting the true structure of the Solar System theoretically.

6. Ptolemy (c.100--c.170 CE) in his book Planetary Hypotheses made an elaborate and valiant attempt to deduce theoretical distances to the astro-bodies, but since the Ptolemaic system (one of those geocentric solar system models) was wrong, he was doomed to failure.

7. Aristarchos of Samos (c.310--c.230 BCE) invented a heliocentric solar system model, and so was on the right track to get the Solar-System distances theoretically in terms of astronomical units (modern value astronomical units (AU) = 1.49597870700*10**11 m), but there is NO historical record of how far got with his model. Eighteen hundred years later, Nicolaus Copernicus (1473--1543), of course, did get the Solar-System distances theoretically in terms of astronomical units using his heliocentric solar system model.