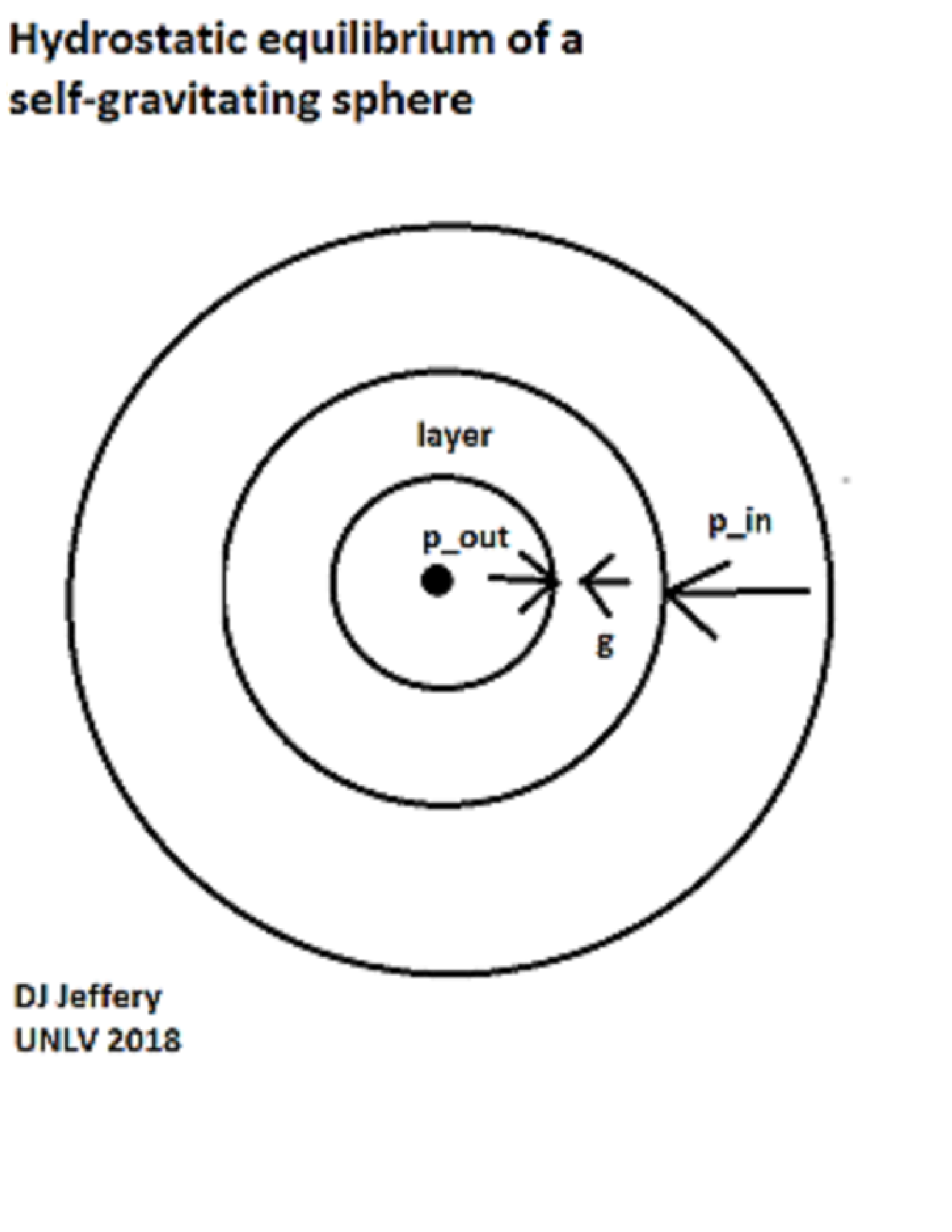
Image 1 Caption: A diagram of spherically symmetric sphere of fluid in hydrostatic equilibrium which in this context means all fluid parcels are at rest (relative to an inertial frame).

Features:

To be at rest, the net force on every fluid parcel must be zero.
To see why a sphere is in hydrostatic equilibrium consider the identified layer in Image 1.
The pressure in the layer is constant, and so there is no tangential pressure gradient to push a fluid parcel in the layer tangentially.
Acting on the layer, we have 3 external forces: pressure outward p_out*A, pressure inward p_in*A, and gravity mg, where A is the surface area of the layer (which is the same to 1st order on both inward and outward sides, m is the layer mass, and g is the gravitational field (which points inward).
For hydrostatic equilibrium (i.e., balance of forces), we find that
```
  p_out*A = mg + p_in*A  
  p_out = (m/A)g + p_in
  p_out = ρg*dr + p_in 
  (dp/dr) = -ρg  , 
```
where dr is the thickness of the layer and ρ is the layer density and (dp/dr) is the pressure gradient---which is negative meaning that pressure decreases going outward. Note, the pressure outward at any spherical shell must support all the mass above the spherical shell, and so pressure increase going inward.
Note, gravity behaves very simply for spherically symmetric mass distributions:
1. It only pulls radially inward toward the center of the distribution.
2. All the mass m(r) contained within a sphere of radius r centered on the center of symmetry acts just as if it were point mass of mass m(r) at the center of symmetry.
3. All the mass outside of the sphere of radius r has NO gravitational effect at all inside the sphere.
4. These great simplifications are due to the inverse-square law nature of gravitational force. The simplifications are summarized in the shell theorem originally derived by Isaac Newton (1643--1727).
The hydrostatic equilibrium spherically symmetric sphere is self-consistent solution for a clump of of a self-gravitating clump of fluid. It is self-consistent since nothing will move with all the forces are balanced, and so the structure is unchanging.
Actually, one has should prove that the hydrostatic equilibrium spherically symmetric sphere is stable: i.e., that vanishingly small perturbations damp out and do NOT cause progressive change to some other structure. We do prove this below actually.
Note, we are assuming surface tension is negligible which is always true on the scale of asteroids and larger. Actually, small liquid drops in free fall are pulled into spherical shapes by surface tension. Also, surface tension does act as a shearing force in many contexts. It prevents liquid drops on a surface from spreading out into an infinitely thin layer.
Now an arbitrary initial clump of fluid (with initially zero macroscopic kinetic energy and zero angular momentum relative to an inertial frame) acting under only self-gravity and pressure will arrange itself into (i.e., relax to) a hydrostatic equilibrium sphere.
Why?
Fluids have very low resistance to shearing forces. The ideal limit of an inviscid fluid (one that has NO viscosity: which is the resistance to shearing forces) has NO resistance at all. But, in fact, as we discuss below, some resistance to shearing forces are needed to make an arbitrary initial clump of fluid relax to a state of hydrostatic equilibrium.
A pair of shearing forces are parallel, but do NOT act along the same line. Thus, they can cause layers of a body to slide relative to each other.
In the case of any initial clump of fluid acted on by self-gravity and pressure acting in combination as shearing forces, fluid parcels will keep moving around until they CANNOT anymore---which is when the clump has relaxed to the self-consistent solution---where there are NO shearing forces acting and NO kinetic energy---which solution is just the hydrostatic equilibrium sphere.
Note, kinetic energy is always being lost due to viscosity (which is the resistance to shearing forces as noted above) which eventually dissipates all the kinetic energy into waste heat.
In astrophysical contexts, the waste heat will usually be radiated away as electromagnetic radiation (EMR).
The fact that self-gravity, pressure, and viscosity always move the clump toward hydrostatic equilibrium sphere proves that that structure is stable. Any perturbation is damped out by the aforesaid self-gravity, pressure, and viscosity.
Note, without some viscosity, there is NO way to dissipate kinetic energy and the clump of fluid will slosh around perpetually and NEVER reach hydrostatic equilibrium.
What if the clump of fluid initially had some angular momentum? This angular momentum will be conserved and the clump will relax to ideally to a uniformly rotating hydrostatic equilibrium oblate spheroid where only the self-gravity, pressure, and centrifugal force are acting. Note, there will also be rotational kinetic energy in the final state in this case.
In the astrophysical realm, the astro-bodies virtually always start formation with some angular momentum, and so virtually always at all stages in existence have some kind of average rotation, unless some process removes all angular momentum, but this virtually NEVER happens.
Now astro-bodies can be made of all fluids (e.g., stars), but they can also be made or partially made of solids like most planets.
But if the self-gravity of a solid is sufficiently strong, the resistance to shearing forces will be so weak that chemical bonds of the solid will eventually break sufficiently and the solid will act as a physics plastic: i.e., it will flow: layers will slide over layers.
When will the flow stop?
Only the pressure force is strong enough to resist sufficiently strong self-gravity. Atoms strongly resist being compressed.
But note the pressure force does NOT resist shearing forces.
So when the pressure force and gravity balance on every small bit of matter flow will essentially stop just described in general above.
Then one has spherically symmetric sphere self-consistent solution.
If there is a centrifugal force due to rotation (relative to an inertial frame), the self-consistent solution becomes approximately an oblate spheroid.
Since almost all pressure-supported astro-bodies have rotation, most pressure-supported astro-bodies with large enough self-gravity to overcome shearing forces are approximately oblate spheroids with usually only a small amount of oblateness: e.g., stars and and planets.
How large does a astro-body have to be pulled into nearly spherical shape?
Well this depends on chemical composition, heat energy content, and rotation.
However, observations suggest the empirical rule that the size scale for a rocky astro-body must be >∼ 600 km and for a water ice astro-body must be >∼ 300 km (see Wikipedia: Dwarf planet: Hydrostatic equilibrium).
Image 2 Caption: The Image 2 shows several structures relevant to our topic. We explicate the structures as follows:
1. A planetary system is supported against its host star's gravity by rotational kinetic energy and angular momentum. Without large macroscopic kinetic energy, astro-bodies become pressure-supported astro-bodies (e.g., stars, planets, and asteroids).
2. Most asteroids have self-gravity too small to pull them into near spheres. Their chemical bonds (aided by pressure and the centrifugal force) allow them to have irregular shapes.
3. The pressure force is strong enough to hold up mountains, but it is isotropic. It pushes equally upward and sideways. The pressure force pushing sideways acts itself as shearing force which is opposed by the chemical bond forces in the rock. However, mountains will slump if the combination of pressure force and gravity can break the chemical bonds of the rock. The slumping stops when the pressure force and gravity are sufficiently reduced that the chemical bonds can resist their shearing forces. Note, mountains on Earth are tiny compared to the Earth because of the Earth's relatively high self-gravity.
4. A typical planet held up mainly by the pressure force with a little centrifugal force that causes the equatorial bulge. There can be little mountains held from slumping by the chemical bonds of the rock.
For a self-gravitating fluid body of UNIFORM density, the exact shape solutions are, depending on conditions, Maclaurin spheriods or Jacobi ellipsoids.
Can there be cases where all possible pressure forces fail to balance self-gravity?
Yes. General relativity (GR) predicts a sufficiently dense massive object will collapse to being black hole with a ring singularity due to rotation (i.e., a Kerr black hole) or a point singularity if there is NO rotation (i.e., a Schwarzschild black hole). The singularities have finite mass and zero volume, and so have infinite density.
However, most people believe that true singularities are avoided by quantum gravity, but we have NO established quantum gravity theory, and so NO established theory of what happens deep in black holes.

Images

Credit/Permission: © David Jeffery, 2018 / Own work.
Image link: Itself.
Credit/Permission: © David Jeffery, 2019 / Own work.
Image link: Itself.

local link: hydrostatic_equilibrium_sphere.html

Fluids file

hydrostatic_equilibrium_sphere.html