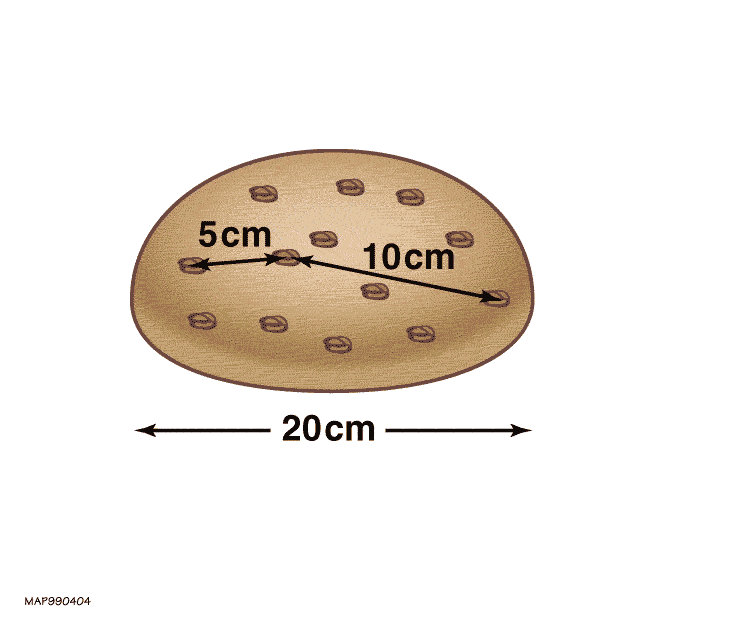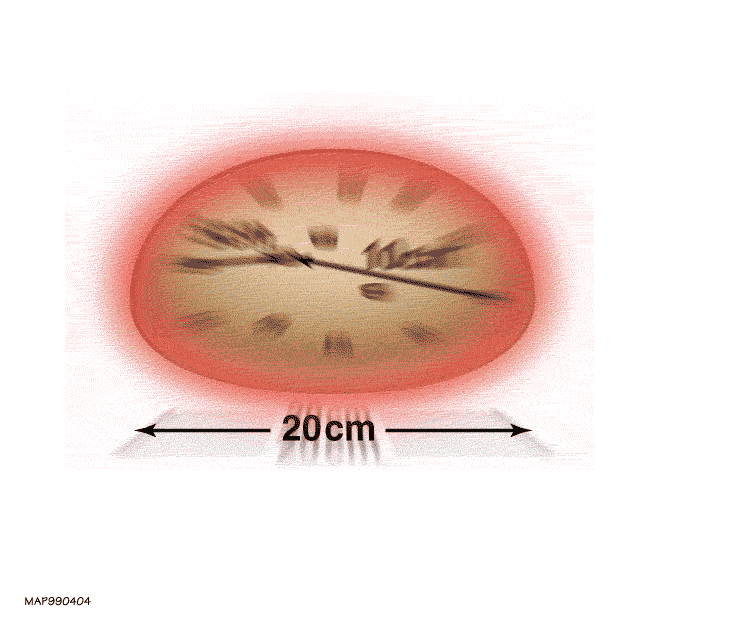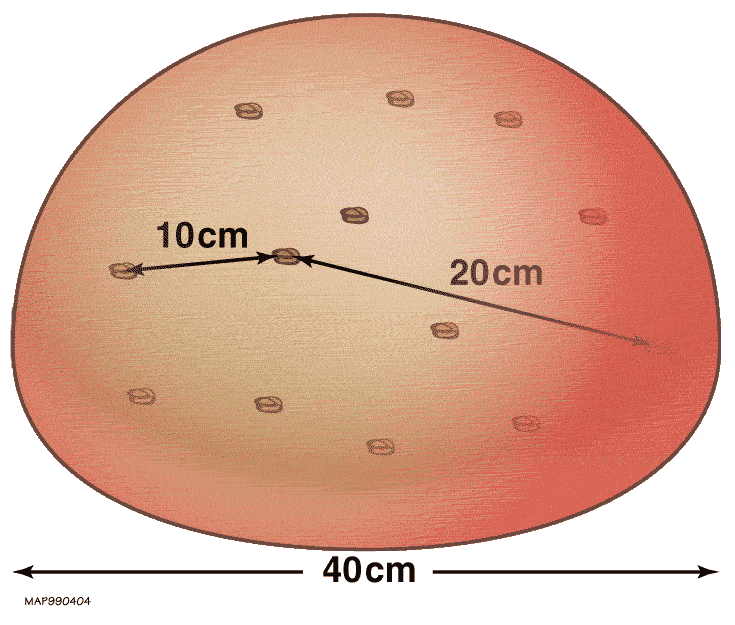
Caption: An animation illustrating that the expansion of an IDEAL loaf of raisin bread when being baked is analogous to the expansion of the universe.

Yours truly is pretty sure real raisin bread does NOT just scale up when baked---but it can be eaten later.

Features:

1. The raisins are like gravitationally-bound systems and other bound systems (like you and me). They don't expand.

2. The basic idea is that all cosmological proper distances (i.e., just ordinary distances measured at one instant in time) between gravitationally-bound systems (and other bound systems) grow with cosmic time (with time zero at the Big Bang) by the cosmic scale factor a(t), where t is cosmic time.

3. The growth of the cosmological proper distances is a literal growth of space according to general relativity.

4. The cosmic scale factor a(t) is common to all growing cosmological proper distances.

   So the structures defined by these cosmological proper distances just scale up with time.

   By convention, a(t=t_0) = a_0 = 1, where t_0 is present cosmic time.

5. At time zero of cosmic time, the cosmic scale factor is zero: i.e., a(t=0) = 0.

   The theoretical time zero is the big bang singularity when the observable universe had zero size and infinite density.

   Actually, no one believes that we can run our cosmological models back to the big bang singularity.

   The observable universe is thought to track into one of those cosmological models a tiny fraction of second after the theoretical time zero (see Wikipedia: Graphical timeline of the Big Bang).

   What came before that tiny fraction of second? That is a story for another figure caption.

6. What is the universe expanding into?

   If the spatial geometry of the whole universe is hyperspherical, then NOTHING. In this case, the universe has the geometry of a 3-dimensional surface of a 4-dimensional n-sphere (AKA hypersphere)---this object is called a 3-sphere (glome).

   The 3-dimensional surface is a finite region with no boundary and the surface is growing with cosmic time.

   The 2-dimensional analogue is the 2-dimensional surface of a growing ordinary sphere.

   We do NOT notice the curved nature of space because we're microbes on a beach ball---it looks flat (i.e., Euclidean) to us.

   What is off the 3-dimensional surface of the 3-sphere? General relativity does NOT say or imply in anyway that space is a 3-sphere in a 4-dimensional mathematical space. It says space has that geometry and nothing more. So There is NO reason to posit anything OFF the curved 3-dimensional surface that is like a 3-sphere. So there's nothing off the 3-dimensional surface and universe is NOT expanding into anything.

7. On the other hand, the whole universe could consist of flat space (AKA Euclidean space) or hyperbolic space.

   In this case, the universe is infinite and the expansion of the universe is a scaling up infinity. This makes mathematical sense---just accept it.

   Once again universe NOT expanding into anything.

8. On the third hand, the observable universe (whatever the shape of space) may be only a tiny part or infinitesimal part of the whole universe most of which is quite different from the observable universe in contents and geometry.

   The most-considered version of this idea is that the whole universe is a multiverse, infinite and eternal, full of pocket universes that are embedded in a background universe. The most-considered version of the multiverse is called eternal inflation with a background universe that is a false-vacuum universe.

   Eternal inflation is nothing like infernal inflation---but isn't a million light-years removed from the cosmology of the Presocratic philosophers Leucippus (first half of 5th century BCE) and Democritus (c. 460--c. 370 BCE) (see Atomist Cosmology (cosmology_atomist.html)).

   In the multiverse theory, our pocket universe (in which the observable universe is embedded) is expanding in the background universe.

   But we do NOT see any hint of the boundary of our (hypothetical) pocket universe. The observable universe seems to obey cosmological principle (i.e., it is homogeneous and isotropic). Thus, we do NOT know where we are in our pocket universe NOR where is its center of expansion if it has one in any sense.