Caption: Cosmological redshift z illustrated.

Features:

1. The redshift (with symbol z) for electromagnetic radiation (EMR) is defined in general by the formula:

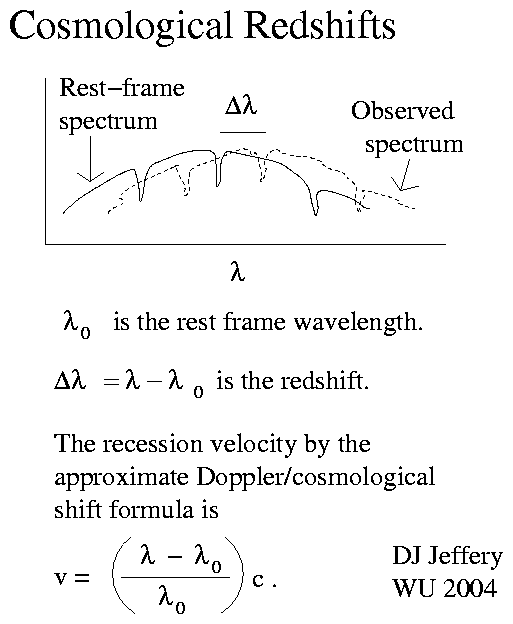
         z=(λ_observed-λ_rest)/λ_rest ,

   where λ_observed is the observed wavelength and λ_rest is the wavelength in the rest frame of emission. Note z is dimensionless number (i.e., it has no units).

2. There are three well known redshifting processes:
   1. The Doppler shift (AKA Doppler effect):

      The Doppler shift is due to the (line-of-sight) relative velocity between two observers one of whom may be a source.

      It is an effect of special relativity and the physical velocities of the two observers relative a single inertial frame which general relativity tells is actually a free-fall frame in a uniform gravitational field. If the specifications are NOT sufficiently well met, corrections to the Doppler effect to get the full redshift are needed.

      The Doppler shift can be a negative redshift in which case it is called a blueshift.

   2. The gravitational redshift: This is a general relativity effect on EMR moving in a gravitational field.

   3. The cosmological redshift:

      The cosmological redshift is caused by an increase in wavelength of EMR due to the literal growth of intergalactic space through which the EMR is propagating. The growing intergalactic space stretches in a sense the EMR waves. The cosmological redshift is an effect of general relativity in expanding universe models.

      Unfortunately, many people conflate the Doppler shift and cosmological redshift.

      They are DIFFERENT, though related, effects and their 1st-order are DIFFERENT in general though the formulae do agree to 1st-order in small recession velocity / relative velocity where the distinction between the two "velocities" disappears (see below). This agreement is what allows the two effects to be conflated often without error, but with mental confusion.

      The agreement of the two formulae to 1st-order allowed early investigators of the universal expansion to interpret their data semi-correctly without being clear about the nature of the universal expansion as a growth of space.

      The conceptual confusion between the cosmological redshift and the Doppler effect was cleared up pretty soon---except for those folks who keep calling the former the latter out of laziness.

      We usually think of the redshift from source to observer. In the expanding universe, there are only positive redshifts due to the cosmological redshift.

      Since wavelength grows with space, the cosmological redshift from cosmic time t in the past to an observer at the present moment cosmic time is given by

        a(t=present)/a(t) = λ_observed/λ_rest  = λ_observed/λ_rest - 1 + 1
      
                          = (λ_observed-λ_rest)/λ_rest + 1
      
                          = z + 1 QED, 

      where a(t) is the cosmic scale factor.

      We can now see why z = ∞ is probably NOT realistic.

      It implies a(t=0) = 0 which means the observable universe started from a region of zero size (i.e., a point) and therefore infinite density.

      We believe that general relativity (or variants thereof) on which cosmological models are based must fail before infinite density is reached.

      Therefore we CANNOT run the clock on these models back to time zero, and therefore they do NOT extend out to z = ∞.

      We can run the models back to a tiny fraction of a second (see Wikipedia: Graphical timeline of the Big Bang).

3. The total redshift is given by

     z_total +1 = (z_receiver + 1)*(z + 1)*(z_source + 1) , 

   where z unsubscripted is the cosmological redshift. If z_receiver and z_source are known, they can be subtracted off. It is often difficult to determine z_receiver and z_source, but almost always they are ≤ ∼ 0.003 (at least for large objects like galaxies and quasars), and so are usually negligible for z >> 0.003: i.e., almost all objects well beyond the Local Group (whose objects have don't participate in the universal expansion relative to us, and so have cosmological redshift z = 0 relative to us).

4. What is called the redshift velocity to an object at cosmological redshift z is defined by the formula:

     v_redshift = zc  , 

   where c is the vacuum light speed c = 2.99792458*10**5 km/s ≅ 3*10**5 km/s . We use units of kilometer per second since they are the natural units in many astrophysical contexts.

   The redshift velocity can be regarded as an ordinary relative velocity between us and the object and as recession velocity to the object to 1st-order in small z.

5. Recession velocity is the true growth in space between us and the observed object at the present instant in cosmic time is NOT an ordinary relative velocity. It can exceed the vacuum light speed which is NOT considered a violation of relativity theory since it is NOT an ordinary relative velocity and no information is traveling at faster than the vacuum light speed.

   According to the Λ-CDM model, recession velocity does, in fact, exceed c for z >≅ 1.

6. The formula for recession velocity is

     v = H_0 * d_p_0 = H_0 * a_0 * g(z)  exactly
       
       = zc*[1-(1/2)(1+q_0)*z] to 2nd-order in small z
    
       = zc = v_redshift to 1st-order in small z, 

   where the subscript 0 indicates the present cosmic time t_0 (i.e., right now where we live), H_0 is the Hubble constant (fiducial value 70 (km/s)/Mpc), d_p is the cosmological physical distance, a_0 is the cosmic scale factor for the present (and is usually defined to be 1) g(z) is a function of z that depends on the cosmological model, and q_0 is the deceleration parameter whose value at present is determined to be nearly -1 (which means the 1st-order formula is nearly 2nd-order good).

   Note that the 1st-order Doppler effect formula for relative velocity v_rel is v_rel = z_Doppler*c, and so the two 1st-order agree for small recession velocity / relative velocity as mentioned above.

7. Note "1st-order-in-small-z" means that a formula is exact neglecting higher powers than 1 in z, and is thus accurate for |z| << 1. In general (though NOT in some special cases) a 1st-order-in-small-z the formula is very inaccurate for |z| approaching or exceeding 1 with a relative error that grows as |z| for |z| << 1.

8. In fact, for the local universe, redshift velocity and recession velocity are often NOT clearly distinguished either for simplicity---as yours truly does---or for confusion.

   Except for the local universe, recession velocity is NOT a direct observable.

   For the local universe, recession velocity is the directly measured as redshift velocity to 1st-order in small z.

   Got that? Yes/No.

9. Cosmological redshift z is a relatively easily direct observable and is common parameter used by astronomers to locate astronomical objects in cosmological spacetime.

   Cosmological physical distance and lookback time are NOT observables. They are model-dependent quantities, and so are NOT good choices for locating astronomical objects in cosmological spacetime.

   Luminosity distance and angular diameter distances are also direct observables, and are very important in determination of cosmological models and their parameters but are NOT nearly as easily obtained as cosmological redshift.

10. Cosmological redshift z is obtained from spectroscopy.

    We can usually measure the emission line and absorption line wavelengths in good quality spectra to high accuracy/precision.

    We recognized the pattern of the emission lines and/or absorption lines, and so know what atoms or molecules they came from.

    Laboratory measurements give us very high accuracy/precision rest frame wavelengths.

    Thus, we can calculate z to high accuracy/precision very often.

11. All EMR from extragalactic sources beyond the Local Group will possess both a Doppler shift due peculiar velocities of source and receiver relative to their respective free-fall frames of the universal expansion and cosmological redshift.

    The Local Group is a gravitationally-bound system physical system, and so the astronomical objects in the Local Group do NOT participate in the universal expansion and NO cosmological redshift or, other words, z = 0 and is the only set of astronomical objects with z = 0.

12. There is NO one definition of the local universe (which is also the relatively contemporary observable universe since the farther you look out the farther you look back in cosmic time), but one useful definition is the region of observable universe at cosmological redshift z ≤ 0.5.

    All cosmological distance measures agree to within a factor of ∼ 2 for z ≤ 0.5 which is a convenient feature. Also the lookback time to z ≅ 0.5 is ∼ 5 Gyr is approximately the age of the Sun (see Wikipedia: Sun). Since we often take the Sun as our standard astronomical object (see, e.g., Wikipedia: Solar units) it is consistent to use to define the local universe using the Sun too.

    Beyond the local universe is the cosmologically-remote observable universe.

    The edge of the observable universe is at z = ∞ by conventional definition.

    In fact, the observable universe probably doesn't go quite that far for reasons we discussed above.

13. The farthest z which we can actually measure to at present is z ≅ 1100 which is when recombination occurred (Wikipedia: Recombination).

    The edge of the observable universe is defined by limit of how far we could see if the pre-recombination epoch were transparent to electromagnetic radiation.

    But it wasn't transparent until the recombination epoch.