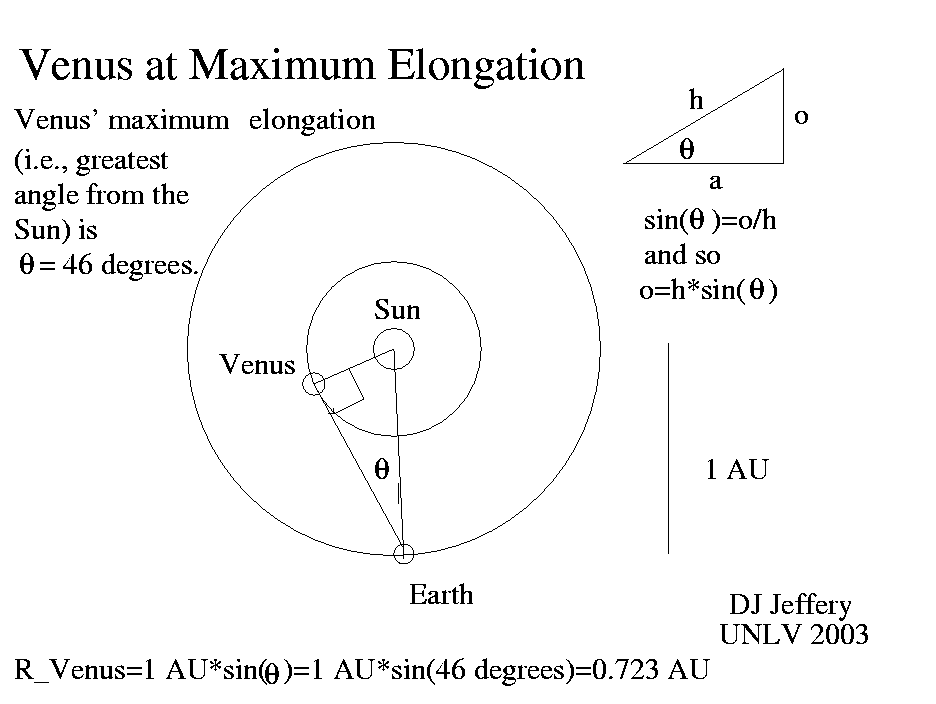
:
- Assume the
planets all orbit the
Sun in
circular orbits.
- When an
inferior planet
is at
greatest elongation,
the line of sight
to the inferior planet
is tangent to the
inferior planet's
circular orbit
and the angle at the
inferior planet
between Sun and
Earth is guaranteed to be
90°.
- Measure the angle of
greatest elongation
θ.
- Now R_(orbital radius)
= (1 astronomical unit)*sin(θ).
- Thus, one can obtain the orbital radii of the
inferior planets
by simple trigonometry
in units of the
astronomical unit.
- The superior planets
orbital radii can also be found with a somewhat more general procedure using
trigonometry.
The procedure is just a bit harder to see at a glance, but it
is easy enough to apply and works for
inferior planets too.
See the
General Procedure for Orbital Radius
Determination
in Orbit file
orbital_radius_determination.html.
- Thus, the hypotheses of
heliocentrism
and circular orbits
allows you to deduce the structure of the
Solar System
(i.e., in Copernicus' day just the distances
to the classical planets, except
for the Moon:
see Moon Distance below) although
the distances are only in the relative unit, the
astronomical unit.
- Also, you got the kinematics
of the Solar System: i.e.,
the description of its speeds
in 3-dimensional space
in astronomical units per
year.
The dynamics
(motions plus causes)
of the Solar System
would have to wait for the advent of
Newtonian physics
with the Isaac Newton's (1643--1727)
book the
Principia (1687).
Discussion:
- In modern science (c.1600--),
theories are judged as powerful
even if they are wrong if they
allow you to deduce important results that can then be tested.
Such theories are honored
as significant achievements.
- Heliocentrism
is a powerful theory in this sense.
- Given heliocentrism,
Copernicus,
was able to obtain results NO ONE had been able to obtain before
(except Ptolemy (c.100--c.170 CE):
see below)
in the historical record
and results were true as it turned out later
(unlike those of Ptolemy (c.100--c.170 CE)
which were derived from
geocentrism).
The heliocentric
distance argument was triumph of the
scientific method
(which had NOT been clearly elucidated in
Copernicus' day).
- Now what of Ptolemy (c.100--c.170 CE)?
He obtained distances to the
classical planets based
hypotheses that loosely followed
from Aristotelian cosmology.
But the hypotheses were themselves
NOT easily tested and were, of course, wrong.
He detailed his theory of
distances in this book
Planetary Hypotheses
which is discussed in
Ptolemy file:
ptolemaic_physical_model.html.
- Was the heliocentric
distance argument known before
Copernicus,
but NOT in the
historical record?
It seems likely that
Aristarchos of Samos (c. 310--c. 230 BCE)
knew it and that is why he proposed
heliocentrism.
See the discussion in
Ancient Astronomy file:
ancient_astronomy/aristarchos.html.
Ptolemy
may have known it since he was such a clever
mathematical astronomer,
but since he rejected
moving Earth
theories as physically absurd
(in Aristotelian physics),
he did NOT bother to discuss it.
- Moon Distance: An interesting point is that
the heliocentric
distance argument does NOT give a distance to the
Moon because
the Moon really does
orbit
the Earth.
In fact, Ptolemy himself
obtained a mean distance to the
Moon of 60.3
Earth radii
(see
Wikipedia:
Hipparchus: Distance, parallax, size of the Moon and the Sun)
which is very close to the modern
Moon mean orbital radius R_Mo = 384,748 km
= 1.28338 light-seconds
= 2.57188 mAU
= 60.3229 R_eq_⊕ ≅ 60 R_eq_⊕ (center-to-center)
(with the Earth equatorial radius R_eq_⊕ = 6378.1370 km).
Since Eratosthenes (c.276--c.195 BCE)
had measured the
Earth radius
fairly accurately,
Ptolemy and
readers of the Almagest
(like Renaissance astronomers
including Copernicus)
did know the distance to the
Moon in terms of
terrestrial distance units.
So somewhat comically,
Copernicus knew the distance to the
Moon
in terrestrial distance units
(in whatever
terrestrial distance units he used:
probably some kind of mile: see
Wikipedia: Mile: Historical), but
NOT in astronomical units (AUs)
and the distances to the other
classical planets
in astronomical units (AUs), but
NOT in terrestrial distance units.
Credit/Permission: ©
David Jeffery,
2003 / Own work.
Image link: Itself.
Local file: local link: venus_elongation.html.
File: Copernicus file:
venus_elongation.html
(AKA
Procedure for Orbital Radius Determination for Inferior Planets).