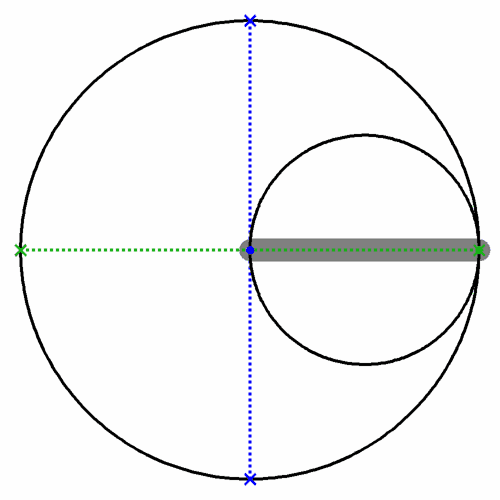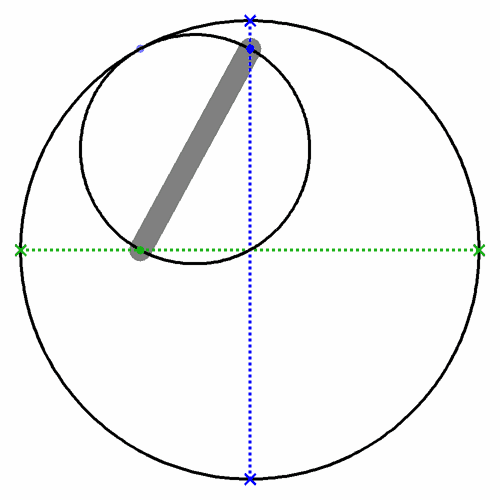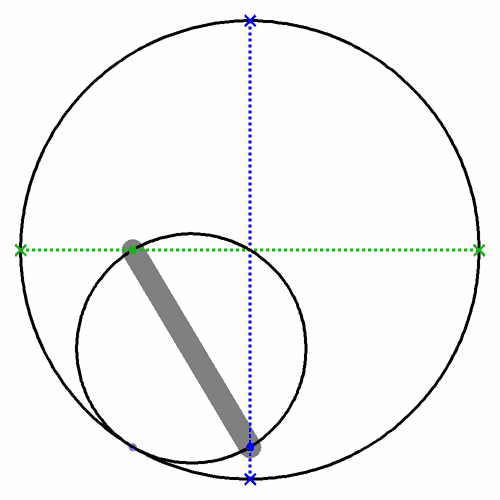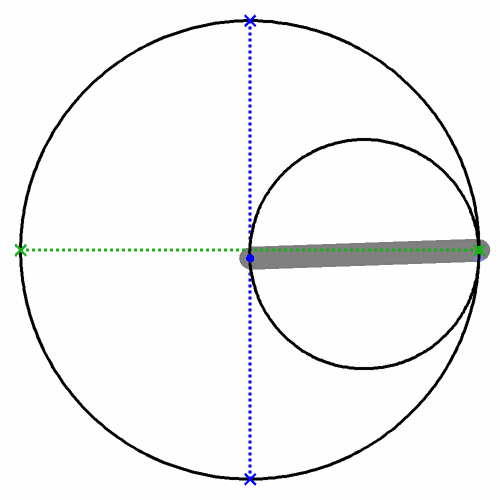
Caption: The Tusi couple (see the animation to the right) is a mathematical device in which a smaller circle (of radius r) rotates around its center while its center rotates (with radius r) around the center of a larger circle twice the diameter of the smaller circle. The compounded motions of the smaller circle cause a point on the circumference of the smaller circle to undergo a sinusoidal oscillation along a diameter of the larger circle. The Tusi couple is a 2-cusped hypocycloid.

Note that along a diameter of any orientation, there will be a sinusoidal oscillation of a some point on the smaller circle. This result follows from symmetry. The animation shows explicitly the sinusoidal oscillations along the x-axis and the y-axis.

Features:

1. The Tusi couple was first introduced in the 13th century by Nasir al-Din al-Tusi (1201--1274) (a Persian polymath: architect, astronomer, mathematician, philosopher, physician, scientist, theologian) in his Tahrir al-Majisti = Commentary on the Almagest (1247) as a model for the latitudinal motion of the inferior planets. It was later often used as a replacement for the equant introduced by Ptolemy (c.100--c.170 CE) in the Almagest. The equant was the crime of Ptolemy since it violated the principle of uniform circular motion which was usually posited as essential by Greek astronomy and by Ptolemy himself.

2. The term Tusi couple is modern and was introduced by science historian Edward Stewart Kennedy (1912--2009) in 1966.

3. Nicolaus Copernicus (1473--1543) made use of the Tusi couple in his planetary models in his De Revolutionibus Orbium Coelestium = On the Revolutions of the Heavenly Spheres (1543).

   It is NOT known how Copernicus knew of the Tusi couple. There are 3 possibilities:

   1. Some more or less complicated transmission path from Nasir al-Din al-Tusi.
   2. Some more or less complicated transmission path from some unknown independent discoverer.
   3. Copernicus may have discovered the Tusi couple for himself---it's not rocket science.

4. The Tusi couple is easily understood with modern Cartesian coordinates expressed as ordered pairs of x coordinates and y-coordinates, trigonometry, and vector formalism:

     vec r_rotation_1= r*(cos(ωt),sin(ωt)) rotation of the center of the smaller circle
                                           relative to the center of the larger circle 
                                           which is the general origin.
                                           ω is the angular velocity.
   
     vec r_rotation_2 = r*(cos(-ωt),sin(-ωt)) = (cos(ωt),-sin(ωt))
                                           rotation of the center of the smaller circle
                                           on its own axis.
                                           ω is the angular velocity.
   
     vec r = vec r_rotation_1 + vec r_rotation_2 = 2r*(cos(ωt),0) net motion of point 
                                           on the surface of the smaller circle. 
                                           For the sinusoidal oscillation,
                                           ω is the angular frequency
                                           and 2r is the amplitude.  

   In fact, the Tusi couple sinusoidal oscillation can be seen as just the x component for any x-axis of a rotation: e.g., the x component of rotation vector

               vec r_rotation = 2r*(cos(ωt),sin(ωt))  .  

5. The transformation of rotation (AKA rotary motion) to sinusoidal oscillation (in technology jargon, reciprocating motion) and vice versa is an important ingredient in technology. For example, the internal combustion engine (ICE) works by converting the reciprocating motion of a piston in an engine cylinder into the rotation of car wheels. See the figure below (local link / general link: internal_combustion_engine.html).

   Yours truly CANNOT think of any exact realization of the Tusi couple in technology.

   ---