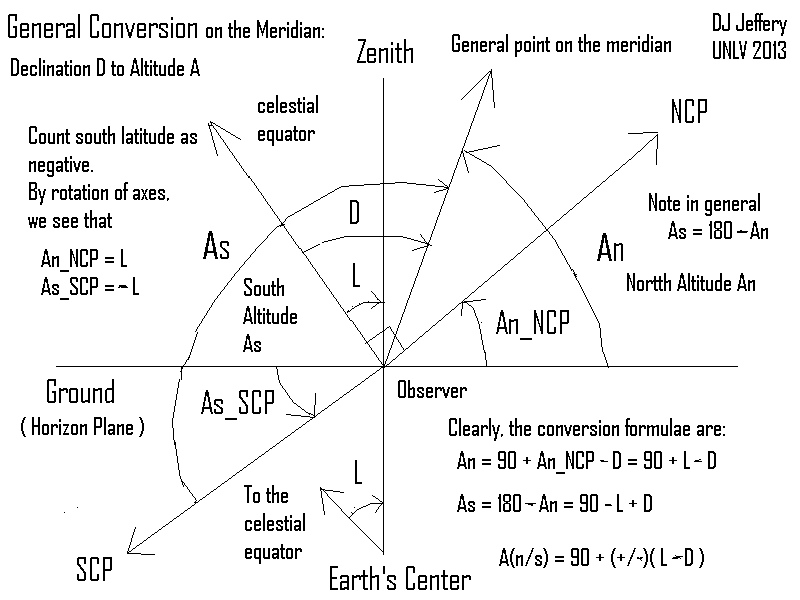
Caption: A diagram proving the general formula for converting the declination (Dec or δ) for a general point on the meridian into an altitude measured either from due north or due south.

Features:

1. It is very easy to measure altitudes to high accuracy.

   It is also easy to convert altitudes measured on the meridian into declinations since you do NOT need to measure multiple angles or use spherical trigonometry.

   Consequently, it is easy to do precise astrometry of astronomical objects during their transits of the meridian.

   In the old days, precise astrometry was always done during transits of the meridian.

2. Here we prove the general formula for converting a meridian altitude into declination using the accompanying diagram.

   The reverse formula follows at once.

3. The general formual and the reverse formula apply for true declination values which are limited to the range [-90°,90°].

   What if one has declination-like angles along the meridian (labeled D in the diagram) that extend outside of the range.

   They can be converted to true declination values with simple rules that we discuss at the last item of the features.

4. Study the diagram.

   Note latitude L is counted as negative for southern latitudes.

   Note An is altitude from due north and As, from due south.

   Obviously in general, As = 180° - An

5. Proof of the general formula we seek:
   1. Lines that go to the celestial equator from any point on the Earth are parallel since the celestial equator is at infinity relative to the Earth.

      Therefore, lines from the Earth's center and the observer going to the celestial equator are parallel.

      The line from the Earth's center to the zenith is a transversal intersecting the aforesaid parallel lines.

      Thus by corresponding angles theorem, the declination of zenith equals the latitude of the observer: i.e., D_zenith = L.

   2. By an obvious rotation of right angles, we see that the altitude from due north/due south of the north celestial pole (NCP)/south celestial pole (SCP) equals latitude/minus latitude: i.e., An_NCP = L and As_SCP = -L.

      By sheer imagination, you can see that this result is true for negative latitudes: i.e., L < 0.

      So everything is general for all latitudes.

   3. The diagram makes the rest of the steps clear. Note D is general declination.

      We have An = 90° + An_NSP - D = 90° + L - D and As = 180 - An = 90° - L + D.

      We can compact the two formula into the general formula we seek:

               A(n/s) = 90° + (±)*(L - D)  , 

      where the upper/lower case is for altitude from due north/due south.

      This completes the proof: QED.

6. As a sanity check, let's see if we can recover from the general formula the altitude from due north/due south NCP/SCP.

   The declination is ± 90°.

   So we obtain, A(n_NCP/s_SCP) = 90° + (±)*[L - (± 90°)] = ± L.

   Which is right. Sanity is proven: QED.

7. The reverse general conversion formula is D = L + (±)*[90 - A(n/s)].

   As a sanity check, let's see if we can recover the declination of zenith.

   Zenith has A(n/s) = 90° for due north/due south.

   Thus, we get D_zenith = L which is correct---sigh, gasp.

8. Now what if we have D values that extend out of the allowed declination range [-90°,90deg;]?

   They can be converted to true declination values with simple, if inelegant, rules.

   Let D' be true declination.

   D = D' for the range [-90°,90deg;], and so D is declination for the range [-90°,90deg;].

   From supplementary angles, if D is in the range [90°,180°], then D = 180° - D' and D' = 180° - D.

   Similarly, if D is in the range [-90°,-180°], then D = -180° - D' and D' = -180° - D.

Credit/Permission: © David Jeffery, 2013 / Own work.
Image link: Itself.
Local file: local link: declination_altitude_inferior.html.
File: Celestial sphere file: declination_altitude_inferior.html.
Superior version: File: Celestial sphere file: declination_altitude.html.