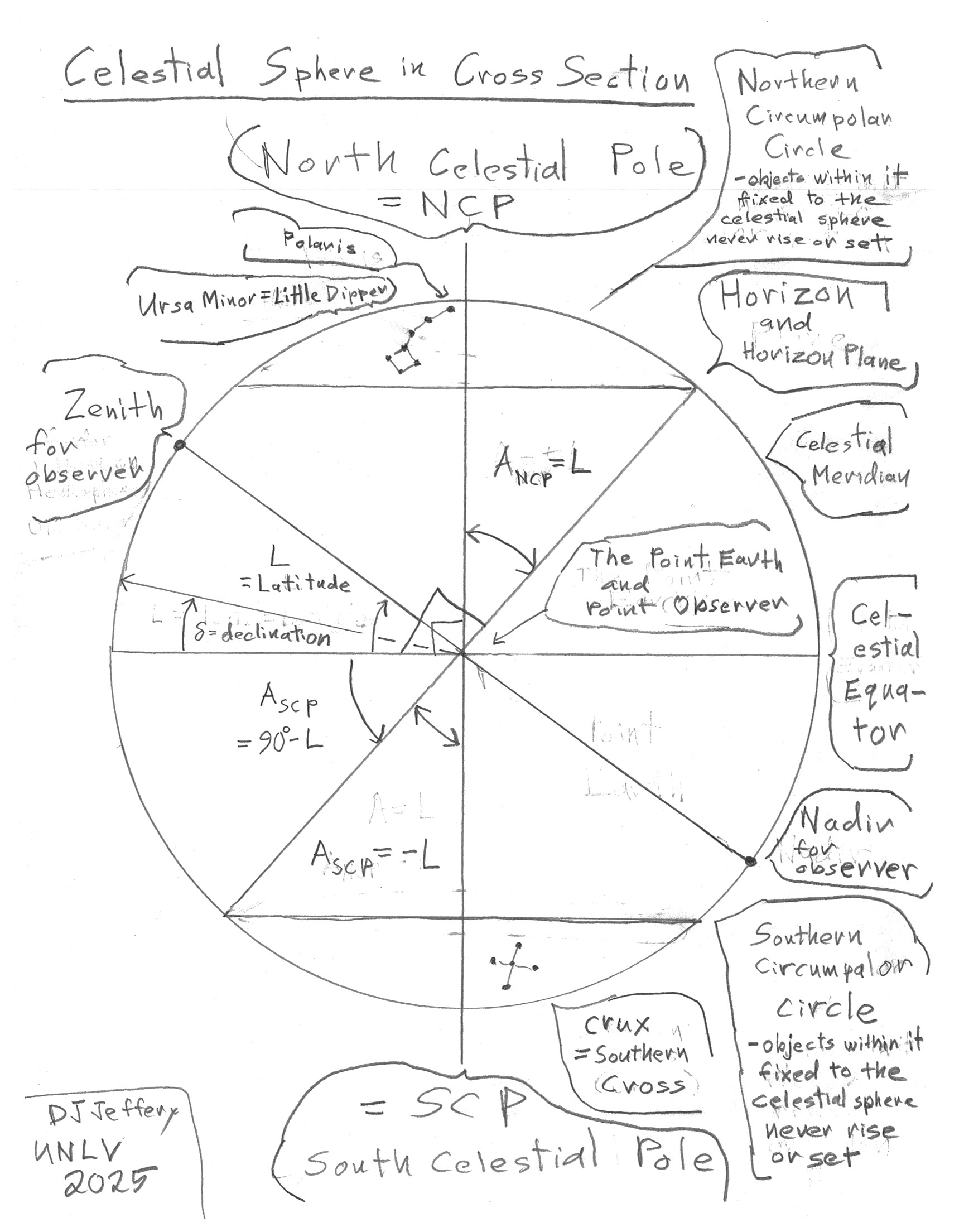
Image 1 Caption: Image 1 The celestial sphere in a cross section diagram (not-to-scale) illustrating the:

point Earth and point observer.
celestial equator.
celestial axis.
north celestial pole (NCP).
south celestial pole (SCP).
celestial meridian (AKA the meridian): a great circle passing through the celestial axis and the observer's zenith. In Image 1, the celestial meridian is coincident with the celestial sphere cross section.
latitude (L) of a point observer located in the cross section plane on the Earth
zenith (nadir) which is the point on the celestial sphere directly above (below) the observer. Nadir is it the antipodal point relative to zenith.
horizon and horizon plane for observer at latitude (L) which is counted positive ( negative) for the observer in the Northern Hemisphere (Southern Hemisphere).
circumpolar sky which is the part of the celestial sphere covered by the circumpolar circles.
circumpolar circles.
circumpolar objects.
circumpolar stars.
declination (Dec,δ).
(astronomic) altitude of the NCP relative to due north A_NCP and of the SCP relative to due south A_SCP. An astronomical object below the horizon has a negative altitude.
constellation Ursa Minor (UMI, Little Dipper).
constellation Crux (Southern Cross).
star Polaris (α UMi) (actually a triple star system).

Features:

The Earth is a point relative to the celestial sphere and the observer on the Earth at latitude (L) is a point relative to the Earth, and so the horizon plane for the observer cuts the celestial sphere in half and the horizon forms great circle on the celestial sphere.
The observer can only see the half of the celestial sphere above the horizon.
Altitude (A) in astronomy is the angle measured from a point on the horizon straight up toward zenith.
Diagrammatically from the rotation of a right angle (90°), it is clear for the observer that the altitudes of the NCP A_NCP and SCP A_SCP are given by the formulae, respectively,
```
   A_NCP = L  and  A_SCP = - L  .
```
Diagrammatically, it is also clear that the absolute value |L| = |A_NCP| = |A_SCP| is the angular radius of the northern and southern circumpolar circles (which are small circles on the celestial sphere).
All astronomical objects within a circumpolar circle are circumpolar objects.
If they are fixed to the celestial sphere, the circumpolar objects NEVER rise or set.
For an observer in the Northern Hemisphere, circumpolar objects fixed to the celestial sphere in the northern (southern) circumpolar circle are always are always above (below) the horizon.
For an observer in the Southern Hemisphere, the situation is reversed.
Of course, circumpolar objects above the horizon may be invisible due to daylight or weather conditions.
Note, some sources (e.g., Wikipedia: Circumpolar star) do NOT consider astronomical objects that are always below the horizon as circumpolar objects---but who cares what they say.
Astronomical objects NOT fixed on the celestial sphere (i.e., Solar System objects: Sun, Moon, planets, artificial satellites, etc.) can change from being circumpolar objects to NOT being circumpolar objects. So they can rise and set.
Note:
1. The remote Solar System objects (e.g., Sun, Moon, planets, remote artificial satellites, etc.) stay circumpolar objects for much longer than a sidereal day = 86164.0905 s = 1 day - 4 m + 4.0905 s (on average), and so their rising and setting periods are much longer than a sidereal day = 86164.0905 s = 1 day - 4 m + 4.0905 s (on average).
  We will call just Solar System objects long-term circumpolar objects.
2. Fast moving low-Earth-orbit artificial satellites can switch from being circumpolar objects to being non-circumpolar objects and time scales much less than a sidereal day = 86164.0905 s = 1 day - 4 m + 4.0905 s (on average), and so can have rising and setting periods much shorter than a sidereal day = 86164.0905 s = 1 day - 4 m + 4.0905 s (on average).
  Note, from Kepler's 3rd law we obtain the for circular orbits the fiducial-value orbital period formulae
```
  p_earth_orbit = 2π/(GM) = (84.4902 ... minutes)*(M/M_⊕)*(R/R_eq_⊕)**(3/2)
                          = (1.40817 ... hours)*(M/M_⊕)*(R/R_eq_⊕)**(3/2)
                         = (0.0586737 ... days)*(M/M_⊕)*(R/R_eq_⊕)**(3/2)  ,
```
  where R is mean orbital radius, gravitational constant G = 6.67430(15)*10**(-11) (MKS units), Earth mass M_⊕ = 5.9722(6)*10**24 kg, and Earth equatorial radius R_eq_⊕ 6378.1370 km.
  It is clear that low-Earth-orbit artificial satellites can rise and set pretty often no matter where they are on the celestial sphere. So there is NOT much interest in whether they are technically circumpolar objects or NOT.
Clearly, circumpolar circles and circumpolar objects are latitude dependent. Note the following consequences:
1. At the Earth's poles (i.e., the North Pole and the South Pole), the circumpolar circles cover the whole celestial sphere: one covers all above the horizon and the other all below. Long-term circumpolar objects just move on small circles around the celestial axis parallel to the horizon with a period relative to the horizon of 1 sidereal day = 86164.0905 s = 1 day - 4 m + 4.0905 s (on average).
  Long-term circumpolar objects will rise and set on long enough time scales.
  The most notable rising and setting long-term circumpolar object is the Sun which rises and sets once per solar year = 365.2421897 days (J2000) at the Earth's poles: it is always above the horizon in the hemisphere summer and always below the horizon in the hemisphere winter.
  In fact, within the Arctic Circle (66.6° N Lat.) and Antacrtic Circle (66.6° S Lat.), there will always be at least a 1 day when the Sun is always a circumpolar object.
2. At the equator, NO astronomical object is a circumpolar object, except artificial satellites in geosynchronous orbit (period = 1 sidereal day, in case of a circular orbit, their orbital radius = 35,786 km = 5.6107 R_equatorial_⊕).
3. The declination of the circumpolar circle at the zenith location is δ = L (which we prove in below section Declination and Altitude).
4. In general, the circumpolar sky increases with absolute value of latitude |L| from 0 % at |L| = 0 to 100 % at |L|=90°.
5. The fraction of sky that is non-circumpolar can all be seen from any given latitude, but only half at any time in the day. The Earth occults the other half: i.e., it is below the horizon . The rotation of Earth allows you to see the whole non-circumpolar sky over the course of a day.

Declination and Altitude:

Declination (Dec,δ) is the angle measured from celestial equator toward the celestial axis. It is positive for the north direction and negative for the south direction. The declination range is δ∈[-90°,90°].
Declination and right ascension (RA) constitute equatorial coordinate system which is analogous to geographical coordinate system latitude and longitude.
Historically, high accuracy/precision declination measurements were done when astronomical objects transited (i.e., crossed) the celestial meridian. Measurements at other times, generally had more error and/or required using spherical trigonometry which is a nuisance.
It is of some interest to relate declination to the altitudes from due north and due south at the time of transiting the celestial meridian.
To do this easily, it is we must define declinations for due north and due south outside of the standard declination range δ∈[-90°,90°]: respectively, these are
```
  δ_dN = L + 90°  and  δ_dS = δ_dN - 180° = L - 90°  
```
where the first formula is obvious from Image 1 and the second formula from the first one.
The altitudes for general declination δ from due north and due south, respectively, are clearly
```
  A_N = -(δ - δ_dN) = -δ + L + 90°  and  A_S = (δ - δ_dS) = δ - L + 90°.  
```
The inverses of these formulae are
```
  δ = -A_N + L + 90°  and  δ = A_S + L - 90°  .
```
For latitude L, we have
```
  L = δ + A_N  - 90°  and  L = δ - A_S + 90°  .
```
Recall, latitude L is given as a negative value for southern latitudes.
The above formulae for the altitudes from due north and due south, their inverses and latitude L look a bit mysterious.
A concrete example can help to believe them. What is the altitude from due south for the Sun in Las Vegas, Nevada on the solstices and equinoxes? Behold:
```
 
   A_S = δ - L + 90°                  In general.
       = δ - 36.2° + 90° = δ + 53.8°  For L_LV ≅ 36.2°.
       = 23.4° + 53.8° = 77.2°        For the summer solstice (∼ Jun21).
       = -23.4° + 53.8° = 30.4°       For the winter solstice (∼ Dec21). 
       = 53.8°                        For the equinoxes (vernal ∼ Mar21, fall ∼ Sep21). 
```
Note, 23.4° is the famous tilt angle of the ecliptic (i.e., the great circle path of the Sun on the celestial sphere in a solar year = 365.2421897 days (J2000)) from the celestial equator. Note also, 23.4° is the Earth's axial tilt (currently 23.4°) (see also Wikipedia: Ecliptic: Obliquity of the ecliptic). On the summer solstice (∼ Jun21) (winter solstice (∼ Dec21)), the Sun is at its highest (lowest) point on the ecliptic and on the equinoxes (vernal ∼ Mar21, fall ∼ Sep21), the Sun is on the celestial equator.
An interesting special case is for the altitudes of the north celestial pole (NCP, δ=90°) and south celestial pole (SCP, δ=-90;). From the general altitude formulae above, we find:
```
  A_N_NCP = L  and  A_S_SCP = - L 
```
Recall, south latitudes are measured as negative. Note, negative altitude means the astro-body is below the horizon.
Another interesting special case is for the declination of the circumpolar circle at the zenith location. In this case, both A_N and A_S are 90° and we find δ = L for both.
Image 2 Caption: The formula A_N_NCP = L is derived directly in Image 2. The formula A_S_SCP = - L follows by mirror reflection symmetry again recalling south latitudes are measured as negative.

Images:

Local file: local link: celestial_sphere_005_circumpolar.html.
Extended File: Celestial sphere file: celestial_sphere_005_circumpolar.html#Declination and Altitude.
File: Celestial sphere file: celestial_sphere_005_circumpolar.html.