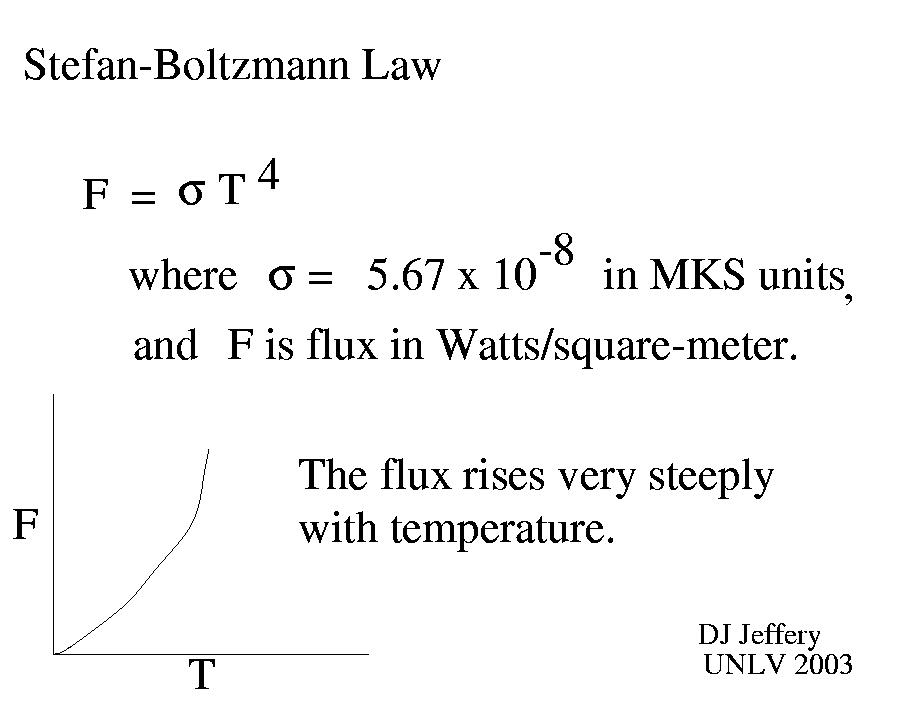
Image 1 Caption: A cartoon explicating the Stefan-Boltzmann law in brief. For a more detailed explication, see below.

Features:

1. The Stefan-Boltzmann law gives the wavelength-integrated flux radiated from the surface of a blackbody radiator.

2. The Stefan-Boltzmann law is

         F = σT⁴   ,

   where F is flux in units of watts (i.e., joules per second) per meter squared, the Stefan-Boltzmann constant σ = (5.67037441918442...)*10**(-8) W/*m**2/K**4 (exact) (see NIST: Fundamental Physical Constants --- Complete Listing 2018 CODATA adjustment), and T is temperature on the Kelvin scale.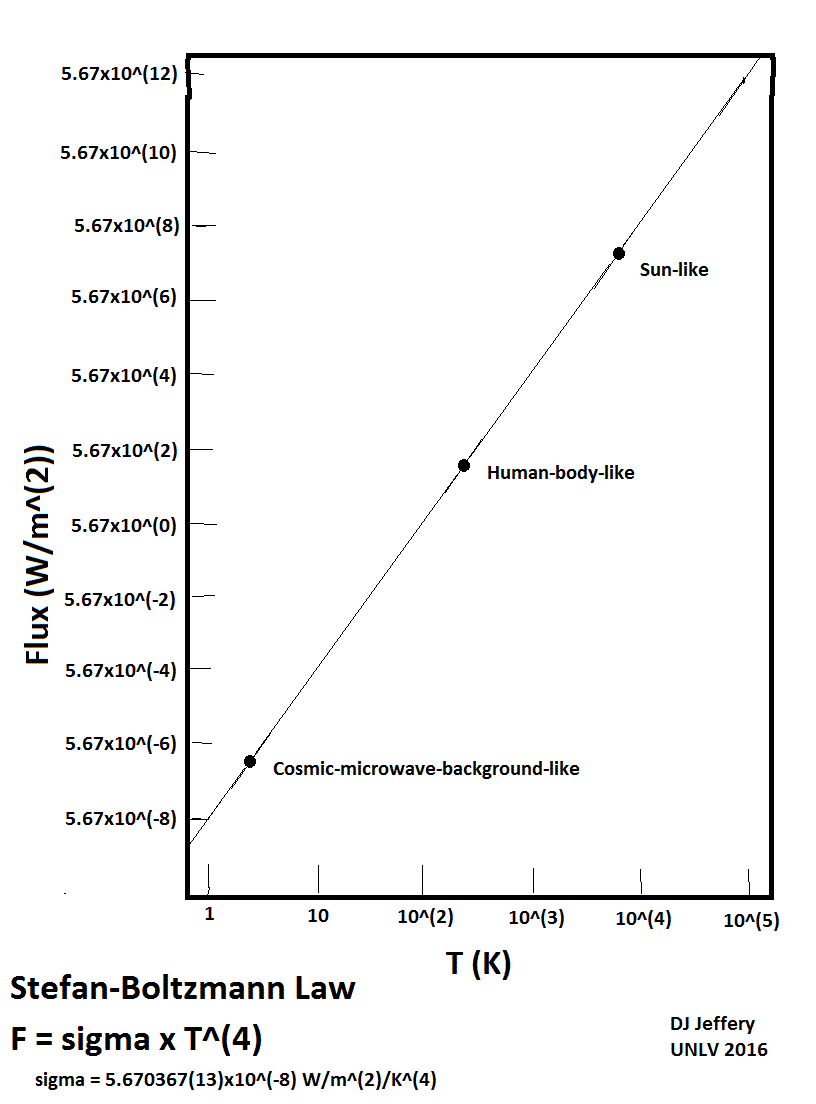

   

3. Image 2 Caption: A log-log plot of the Stefan-Boltzmann law.

4. The plot is NOT highly accurate/precise since it was drawn semi-freehand.

5. We can see that radiant flux F increasing as the 4th power of temperature---a very strong increase with temperature.

6. Since this is log-log plot, the Stefan-Boltzmann law appears a straight line with slope = 4 (which is the exponent (AKA power) of the Stefan-Boltzmann law) and y-intercept at T = 1 K equal to the Stefan-Boltzmann constant itself.

   The logarithmic Stefan-Boltzmann law is

         log(F) = log(σ) + 4log(T) ,

7. The labeled points are approximately where identified like objects would be located if they were blackbody radiators. Below, see Table: Blackbody Radiators.

8. Image 3 Caption: Ludwig Boltzmann (1844--1906) in 1902.

   
   
   
   
   
   

9. Table: Blackbody Radiators:

   
     Table:  Blackbody Radiators
   
     Blackbody Radiator        T            F           Comment
                              (K)       (W/m**2)
   
     CMB-like                2.7260    3.131*10**(-6)   The CMB has a blackbody spectrum, 
                                                        but there is no radiating surface 
                                                        in the modern observable universe.
     Human-body-like       310         5.237*10**2      But the human body does NOT radiate 
                                                        this much (see the note below).
     Sun-like             5772         6.294*10**7      The Sun does almost radiate 
                                                        like this at the
                                                        effective temperature T = 5772 K.  

   ---

   Keywords: basal metabolic rate (BMR), basal metabolic rate average ≅ 73 W, blackbody radiator, cosmic microwave background (CMB), effective temperature, effective temperature of the Sun, flux, heat energy, human body, human body temperature, Kelvin temperature scale, Stefan-Boltzmann constant, Stefan-Boltzmann law F = σT**4, Sun, temperature, watts.
   References: NASA Sun Fact Sheet for the Sun's effective temperature. The value of the effective temperature varies a bit depending on reference.
   

   ---

10. Effective Temperature and Color Temperature:

    The effective temperature T_eff of a star is the temperature of a blackbody radiator that radiated exactly the luminosity L of the star from a spherical surface of exactly a well-defined characteristic radius for the star's photosphere: i.e., the photospheric radius R_ph. The formulae for effective temperature are:

      L = (4πR_ph)*F = (4πR_ph)*σT_eff**4  and T_eff = [L/(4πR_ph*σ)]**(1/4)  ,

    where we have used the Stefan-Boltzmann law F=σ*T**4 for blackbody radiation. However, there are complications in evaluating effective temperature:
    1. How do you define photospheric radius exactly. Definitions may vary depending on reference.
    2. How do you determine luminosity exactly?
    There are various ways of dealing with these complications which are beyond our scope.
          What is called the color temperature of a star is based on fitting a blackbody spectrum to the star's spectrum. There are various ways of the doing the fit which give somewhat different answers. The fit can be done using Wien's law or color indices.
          Since a star is NOT exactly a blackbody radiator with a radius equal to the aforesaid well-defined characteristic photospheric radius, the color temperature will NOT in general equal the effective temperature. In fact, the color temperature is usually a bit higher.
          The effective temperature is preferred over color temperature for the definition of the standard photospheric temperature because the effective temperature has a perfectly meaning for a photosphere in special ideal case that many stars actually approach: i.e., the case of a grey atmosphere in local thermodynamic equilibrium (LTE) (Wikipedia: Grey atmosphere: Temperature solution; Mi-55,72).
          The temperature for the Sun given in Table: Blackbody Radiators 5772 K is the effective temperature. For the Sun, the color temperature (from some determination method) is ∼ 5900 K (Wikipedia: Color temperature: Sun) which is, indeed, a bit higher than the Sun effective temperature 5772 K.

    In general, the effective temperature is harder to determine than color temperature.

11. We can expand a bit on the human-body-like blackbody radiator in the above Table: Blackbody Radiators.

    A human body approximated as a cylinder has surface area ∼ h*2πr ≅ 1.5*6*0.2 ≅ 2 m**2. Thus, according to the above table if it radiated like a blackbody radiator, it should radiate ∼ 1000 W. But the human body is surrounded by an ambient medium at typically ∼ 300 K and the radiation field and heat conduction from the ambient medium is sufficient to transfer heat to the human body to maintain a temperature ∼ 300 K. Upshot is that the human body radiates a DILUTED blackbody radiation field: it has approximately a blackbody spectrum shape for temperature ∼310 K, but has much less radiant flux than a blackbody radiation field of ∼310 K. So the human body does NOT lose heat energy at rate of ∼ 1000 W.

    But how much radiant flux does the human body radiate? The basal metabolic rate (BMR) for humans is the minimal rate of energy generation in and therefore the minimal heat energy loss from the human body. The energy generation comes from food energy (i.e., the chemical energy of food). The basal metabolic rate average ≅ 73 W is obviously much less than the flux from the human-body-like blackbody radiator in the above Table: Blackbody Radiators.

    For some information from 2019 on the human body metabolic rate, see BBC: Ultimate limit of human endurance found, 2019, Thurber et al. (2019), and references therein.

Images:

1. Credit/Permission: © David Jeffery, 2003 / Own work.
   Image link: Itself.
   
2. Credit/Permission: © David Jeffery, 2016 / Own work.
   Image link: Itself.
   
3. Credit/Permission: Anonymous photographer, 1902 (uploaded to Wikimedia Commons Wikipedia by User:JDH, 2006) / Public domain.