


Next: Unitary operators
Up: Bra-ket notation
Previous: Projection operators
Above we suggested that operators in Hilbert
space can be written as a sum of outer products. However, it
is much easier to work with operators that are expressed as
matrices. Given operator Y and
a basis set of kets
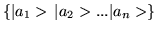 ,
we can construct an
,
we can construct an
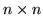 table of complex numbers whose
table of complex numbers whose 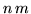 th
element is given by
<an| Y | am>. The set of n2 complex
numbers can most conveniently be written as a square matrix, where m is
a column index and n a row index. We use
the notation
th
element is given by
<an| Y | am>. The set of n2 complex
numbers can most conveniently be written as a square matrix, where m is
a column index and n a row index. We use
the notation
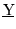 to represent this matrix, and
the
to represent this matrix, and
the 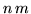 th element of that matrix
is
th element of that matrix
is
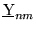 .
The matrix
.
The matrix
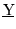 is called
the matrix representation of operator Y. Show that we
can express Y in the form
is called
the matrix representation of operator Y. Show that we
can express Y in the form
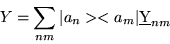 |
(1.39) |
Consider the following equation in ket space,
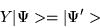 |
(1.40) |
where Y is an operator and 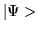 an arbitrary ket.
We take the inner product of this equation with state | am>(Remember, taking an inner product of two kets involves multiplying
on the left by a bra), or
an arbitrary ket.
We take the inner product of this equation with state | am>(Remember, taking an inner product of two kets involves multiplying
on the left by a bra), or
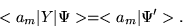 |
(1.41) |
Evaluating this expression we obtain,
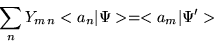 |
(1.42) |
which can be written as a matrix equation
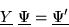 |
(1.43) |
where we defined a column matrix
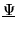 whose
n'th row has the entry
whose
n'th row has the entry
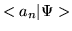 .
The utility of a matrix representation for operator
Y and ket
.
The utility of a matrix representation for operator
Y and ket 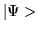 is now apparent.
We can replace any abstract operator equation, such as
Eq. (17), with a more familiar matrix equation (20).
is now apparent.
We can replace any abstract operator equation, such as
Eq. (17), with a more familiar matrix equation (20).
We can do the same in bra space. For example, consider
the adjoint of Eq. (17)
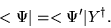 |
(1.44) |
Show that the matrix representation of this equation is given
by
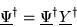 |
(1.45) |
where
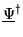 is the adjoint matrix
of the column matrix
is the adjoint matrix
of the column matrix
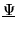 (note:
you can consider the adjoint of a column matrix
to be a row matrix). Note that the n m 'th element of
matrix
(note:
you can consider the adjoint of a column matrix
to be a row matrix). Note that the n m 'th element of
matrix
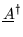 is the complex conjugate
of the m n'th element of matrix
is the complex conjugate
of the m n'th element of matrix
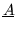 ,
i.e.
,
i.e.
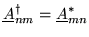



Next: Unitary operators
Up: Bra-ket notation
Previous: Projection operators
Bernard Zygelman
1999-09-21
![]() ,
we can construct an
,
we can construct an
![]() table of complex numbers whose
table of complex numbers whose ![]() th
element is given by
<an| Y | am>. The set of n2 complex
numbers can most conveniently be written as a square matrix, where m is
a column index and n a row index. We use
the notation
th
element is given by
<an| Y | am>. The set of n2 complex
numbers can most conveniently be written as a square matrix, where m is
a column index and n a row index. We use
the notation
![]() to represent this matrix, and
the
to represent this matrix, and
the ![]() th element of that matrix
is
th element of that matrix
is
![]() .
The matrix
.
The matrix
![]() is called
the matrix representation of operator Y. Show that we
can express Y in the form
is called
the matrix representation of operator Y. Show that we
can express Y in the form