


Next: Matrix representation of operators
Up: Bra-ket notation
Previous: Bra-ket notation
Armed with the bra-ket formalism we can construct any operator
in Hilbert space. The projection operator Pa is defined
as
Note that
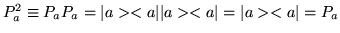 and in general any projection operator P has the property
P2=P. Consider operator X whose eigenstates are given
by the set
and in general any projection operator P has the property
P2=P. Consider operator X whose eigenstates are given
by the set
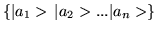 .
If we
define the projection operators
Pan = | an><an|, show that
operator X can be expressed as a sum of projection operators, i.e.
.
If we
define the projection operators
Pan = | an><an|, show that
operator X can be expressed as a sum of projection operators, i.e.
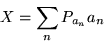 |
(1.38) |
Bernard Zygelman
1999-09-21