3 Electronic structure

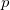The atomic orbital contributions plotted in Fig. 5.3 exactly sum up to the total DOS and thus, when integrated up to the Fermi level, represent the fraction of valence electrons that occupy the corresponding set of atomic orbitals. Note that the contribution of Xe $s$ and $p$ set of orbitals strongly decreases on going from left to right in Fig. 5.3 because of two concurring effects, the change in stoichiometry (from a Xe:O ratio of 1 down to 1/3) and the parallel enhanced electron transfer from Xe to O (Xe Bader charges being +1.01 in XeO, +1.995 on average in XeO $_2$ and +2.754 in XeO $_3$ ). To help the reader to disentangle the effect of stoichiometry from that of the increasing charge transfer, the same DOS shown in Fig. 5.3, but with contributions from Xe orbitals multiplied as to counterbalance the stoichiometry change, are shown in Fig. 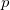9.5, which clearly displays a trend that the ratio of O $p$ orbitals’ contribution to Xe 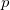$p$ orbitals’ contribution below Fermi energy increases as stoichiometry changes from XeO to XeO $_3$ . 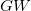For comparison, the $GW$ DOS plot is also shown in Fig. 9.6.

$\includegraphics[scale=0.5]{pdf/dos.png}$

Figure 9.5: Total density of states for a) XeO-Pbcm at 100 GPa, b) XeO $_2$ -P2 $_1$ /c at 150 GPa, c) XeO $_3$ -Pmmn at 200 GPa together with their projections on the set of orbitals of the atoms. The contributions from Xe orbitals have been multiplied by two in XeO $_2$ and by three in XeO $_3$ to show the relative contribution from each kind of atoms. At variance with Fig. 5.3 in chapter 5, the sum over the plotted projections does not yield the total DOS.

$\includegraphics[scale=0.5]{pdf/GW.png}$

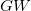Figure 9.6: Total $GW$ density of states for a) XeO-Pbcm at 100 GPa, b) XeO $_2$ -P2 $_1$ /c at 150 GPa, c) XeO $_3$ -Pmmn at 200 GPa.