Crystal Structure Prediction and its Application in Earth and Materials Sciences: Fingerprint: to prevent premature convergence

1.5 Fingerprint: to prevent premature convergence

A general challenge for global optimization methods is to avoid getting stuck in a funnel around some local minima but not the global minimum. This is due to the fact that good structures tend to produce children in their vicinity. Such behavior is especially common for energy landscapes with many good local minima. To prevent this so called premature convergence, the key is to control the diversity of the population, i.e. we do not want the whole population is located in one basin. Thus one question comes up - how can we detect similar structures and measure the similarity quantitatively?

Direct comparison of atomic coordinates will not work because they are represented in lattice vectors units and there are many equivalent ways to choose a unit cell. Free energy difference is not good parameter as well (two completely structures can have very close energy like graphite and diamond). An ideal solution should be 1) derived from the structure itself, rather than its properties, 2) invariant with respect to shifts, rotation, and reflections in the coordinate system; 3) sensitive to different orderings of the atoms; 4) formally related to experiment; 5) robust against numerical errors. In USPEX, we use so-called fingerprint function ²⁸ to describe a crystal structure. It has the formulation very similar to radial distribution function (RDF):

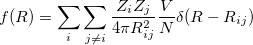$\begin{equation} f(R)=\sum _ i\sum _{j \neq i}\frac{Z_ i Z_ j}{4 \pi R_{ij}^2}\frac{V}{N}\delta (R-R_{ij}) \end{equation}$

(5)

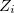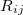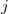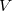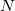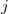where $Z_ i$ is the atomic number for atom $i$ , $R_{ij}$ is the distance between atoms $i$ and $j$ , $V$ is the unit cell volume, and $N$ is the number of atoms in the unit cell. The index $i$ goes over all atoms in the unit cell and index $j$ goes over all atoms within the cutoff distance from the atom $i$ . To remove the fingerprint dependency from cutoff distance, the function is normalized as:

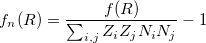$\begin{equation} f_ n(R)=\frac{f(R)}{\sum _{i,j}Z_ i Z_ j N_ i N_ j} - 1 \end{equation}$

(6)

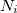where $N_ i$ is the number of atoms in the unit cell with atomic number $Z_ i$ .

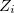One could measure the similarity between structures by calculating the cosine distance between two fingerprint functions,

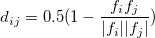$\begin{equation} d_{ij}=0.5(1-\frac{f_ i f_ j}{|f_ i||f_ j|}) \end{equation}$

(7)

Using this new crystallographic descriptor, we can improve the selection rules and variations above. During the selection process, we ignore all similar structures and only choose different ones. There are some other benefits from fingerprint theory, one could find the details in Ref. ²⁸.