Phase Changes
Bulk
phase changes (or transitions) for a pure substance happen at
definite temperatures
which---just to make life complicated---are dependent on
pressure.
To get a phase change
at the temperature specified
for the material,
the sample must have the constant
temperature in space
as the transition occurs.
If there are a range of temperatures
in the sample,
then the situation is more complex obviously.
Nevertheless, in many typical and not well-controlled cases,
the bulk phase changes
will happen at nearly the
temperatures
specified for the material.
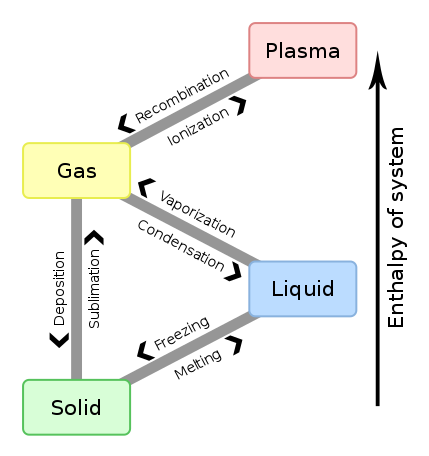
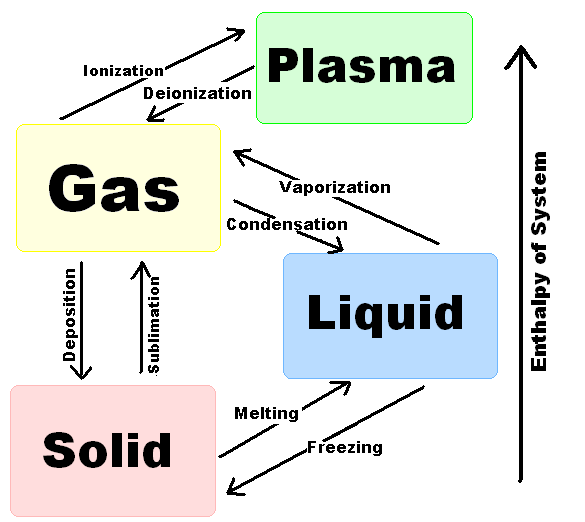
The order of changes with increasing temperature is
solid
to
liquid
to
gas.
The change (reverse change) from
solid
to
liquid
is melting (freezing).
The change (reverse change) from
liquid
to
gas
is evaporation (condensation).
The direct change (direct reverse change) from
solid
to
gas
is formally sublimation (deposition).
Actually many people---like yours truly and other astrophysicists---loosely use evaporation and condensation
for, respectively, sublimation and deposition.
The phase change temperatures generally INCREASE with
increasing pressure.
It is a good mnemonic to say that increased pressure
usually likes to keep matter in the usually denser phase.
This is true loosely speaking.
The higher the pressure increases the strength of the
chemical bonds
and a higher temperature (implying greater microscopic kinetic energy)
is required to break/change the bonds.
Of course, then phase change temperatures generally DECREASE with
decreasing pressure.
This is actually a problem if you want really hot coffee at high altitude.
Water boils at 100 degrees C (373 K) at standard pressure (about 0.1 MPa).
On the peak of Mount Everest
the pressure is about (0.026 MPa) and
the boiling point of water is only about 69 degrees C (342 K)
(
Wikipedia: Boiling Point).
Once water starts boiling it won't get any hotter than the boiling point
since all the added internal energy
goes into evaporating the
water as we will discuss below.
Unless boiled under pressure, real hot coffee is difficult at high
altitude.
``Yes sir, nothing like lukewarm coffee after a day of climbing in sub-freezing
conditions in a blizzard.''
Of course, you could take your own
espresso machine
with you on the ascent.
Under sufficiently low pressure,
the whole liquid phase gets skipped and
a solid
will phase change directly to
a gas.
What low pressure
depends on the
substance.
Most
familiar substances
have a liquid phase
under ordinary
air pressure.
There as some noteworthy ones that do NOT.
Question: Why is
dry ice
called
dry ice?
- No good reason.
- It is a
genericized trademark.
- At ordinary pressure it doesn't be come a fluid.
- All of the above.
Answer 3, I guess, but
Wikipedia: Dry Ice
is not explicit on this point.
The name dry ice
is a
genericized trademark too by the way.
To paraphrase Will
Rogers (1879--1935), all I know is what I read in
Wikipedia.
Actually, dry ice
is a very effective coolant since it is colder than
ice (water ice) (i.e., it's at -78 degrees C = 195 K)
and it is convenient since doesn't leave any moisture.
It is easy to buy commercially.
But you can
frostbite from it, and so some caution is needed in handling.
There is another extreme case of
pressure.
At very high
pressures
the distinction between
liquids
and
gases
vanishes.
You know longer see an interface between the
denser and less dense parts of what
can be just called the fluid phase.
It takes significant
internal energy
to break the
chemical bonds
when a sample is
undergoing a phase change.
Question: Melting a sample of
ice takes about as much energy as raising liquid water's
temperature by ____________ degrees Celsius.
- 80
- 1
- 800
- All of the above.
Answer 1 is right:
specific latent heat of fusion / specific heat
= 333 kJ/kg / 4.190 kJ/(kg C) = approximately 80 C.
Adding
internal energy
when a sample is undergoing a phase
change tends to
go into breaking the bonds
chemical bonds
and not into increasing
temperature.
If you added the
internal energy
very uniformly and slowly to the sample,
you could keep the whole sample at the phase change temperature and have
all the added
internal energy
go into breaking the
chemical bonds:
i.e., into causing the
phase change.
It's hard to arrange this to happen perfectly, but not
so hard to do it approximately.
This is why the
liquid water
in
ice water
tends to stay ice-cold: i.e., near the freezing temperature
of water (at about 0 degrees C = 273.15 K, but there is some
pressure dependence) as long as any
ice
persists in the sample.
This is also why boiling water won't get hotter than
boiling temperature.
Virtually all
the added
internal energy
goes into
breaking the
chemical bonds.
Only after all the liquid water is gone will the inside of the container
be able to get much hotter than the boiling point.
This, of course, is why it is hard to
get hot coffee
on the peak of
Mount Everest
as mentioned above.

Ice undergoing a phase change to water at approximately a
constant overall temperature near 273.15 K = 0 degrees C.
The lemon is essentially a bystander---but decorative.
Credit: Jon Sullivan of
PD Photo.org. The author has released the
image into the public domain.
Download site:
Wikipedia: Image:Ice water.jpg.
Now the melting and boiling temperatures are the melting and boiling
for bulk samples where the samples are all at the same
temperature
for the ideal behavior.
At the surface of any surface of any sample of
solid
or
liquid,
the individual
atoms
or
molecules
have a distribution of
thermal energies.
There will always be some
atoms
or
molecules
that can break
chemical bonds
and escape from the surface.
But
atoms
or
molecules
in the phase of escape can also
land on the surface and rebond if their individual
thermal energies
are low.
There is, in fact, a continual flow of escapees and returnees
at surfaces.
For example, at the surface of a
liquid,
if the gross evaporation rate exceeds the
gross condensation rate, there
will be a net evaporation rate
and the sample of
liquid
will evaporate even at temperatures well
below the boiling temperature.
The rates of escape and return depend on many things, but
a key one is the density of the
atoms
or
molecules
in the phase of escape.
We see this all the time with water: samples of water
evaporate as long as the
relative humidity
is less than 100 %.
Just as evaporation
can happen well below the boiling temperature, so
sublimation
can happen will below the melting temperature.
We have all seen this with
ice
and
snow.
It vanishes even if the temperature stays sub-freezing.
Especially if the there is bright sunlight
(in other words radiant energy)
to give
internal energy.

Ice surfing on the Znin Small Lake.
See Znin, Poland.
Ice forms on the top of water bodies, because it is less dense than liquid water.
Usually the solid phase is denser than the liquid.
That this is not so for water is one of water's remarkable properties.
At 0 degrees C, ice has density density 0.9167 g/cm**3 but
liquid water has density 0.9998 g/cm**3.
Liquid water density reaches a maximum of 1.00 g/cm**3 at 4 degrees C
(
Wikipedia: Ice).
These precise numbers are for a air at 1 atmosphere air pressure
(0.101325 Mpa) (I think).
As liquid water passes below 4 degrees C it becomes more buoyant than warmer
water (because less dense) and tends to rise and reach the surface where it freezes or it
could freeze and float to the surface.
Icebergs float likewise
because ice is less dense than liquid water.
Credit:
Wikipedia contributor Andrej Luczak.
According to
Wikipedia
permission is granted to copy, distribute and/or modify this document
under the terms of the
GNU Free Documentation License, Version 1.2 or any later version.
Download site:
Wikipedia: Image:Ice surfing.jpg.
It is possible to see all three (main)
phases of matter at once.
But this will not be a
system in overall
thermodynamic equilibrium usually.
It will be a state of thermodynamic non-equalibrium which means that
the system
will changing in time or will be in some steady state with
inflows and outflows of
energy
and/or matter in some form.
For example, we do see the three phases of
water at the same
time in a system---cough---not in
thermodynamic equilibrium
When evaporation
happens from surfaces below the boiling temperature, there is
a strong cooling effect.
Evaporative cooling
occurs because the evaporation process takes significant
internal energy
from the surroundings in order to cause the escape of the
atoms
or
molecules.
Evaporative cooling
is a vital process in making
refrigerators
work as we will discuss
in lecture
Heat Engines,
Refrigerators, and the Carnot Heat Engine (section Refrigerators).
Evaporative cooling
is also important to life.
Mammals, for example,
can cool by
sweating.
Water is emitted from the skin and evaporates causing a cooling effect.
Humans
are the grand champion sweaters, in fact.
Our maximum water perspiration rate is over 500 g/(m**2*h)
(Smil 2006, p. 61).
Our sweat potential gives humans
a tremendous ability to be active and work while most other
mammals
and other critters are flaked out.
In South African gold mines, miners at 3 km down work in
temperatures of 50 degrees C
(Smil 2006, p. 61).
Workers in 18--19th century iron foundries may have endured
similar temperatures
(Cardwell 1994, p. 171):
they worked in the
Inferno.

Caption: "Dante's guide rebuffs Malacoda and his fiends in Inferno Canto 21 between ditches five and
six in the eight circle."
Credit: Gustave Dore (1832-1883).
Linked source: Wikipedia
image
http://en.wikipedia.org/wiki/Image:Gustave_Dore_Inferno_Canto_21.jpg.
Public domain.
Other mammals
are way down.
Camels---those
ships of the desert---max out at about 250 g/(m**2*h).
Horses
can do about 100 g/(m**2*h).
And then there are canids.

The
Irish wolfhound who is the mascot of
Irish Guards who are evidently in the British Army.
The
Irish wolfhound
is the tallest breed of dog with an average height at the withers of
90 cm (34 inches).
Canids
(which include dogs)
don't sweat (or so my source
tells me).
They pant and tongue-loll to make use of evaporative cooling from
the somewhat inner surfaces of their bodies
(Smil 2006, p. 61).
Credit: Wikipedia
contributor Elf.
According to
Wikipedia
permission is granted to copy, distribute and/or modify this document
under the terms of the
GNU Free Documentation License, Version 1.2 or any later version.
Download site:
Wikipedia: Image:Wolfhound mascot wb.jpg.
``And that's all folks for phase changes"---as
Bugs Bunny
used to say.