Mass-Energy Equivalence or E=mc**2
Albert
Einstein (1879--1955) circa 1905.
He was always a flashy dresser.
Credit: unknown.
Download site: unknown.
This picture was obviously taken in the first decade of the
20th century and by
U.S. copyright law is now out of copyright.
According to the informative, but not authoritative, source
WebMuseum, Paris copyright in all other
jurisdictions would have expired
if the holder died more than 70 years ago.
In 1905,
Einstein
published three famous papers including the one on
special relativity with all of its predictions for the
dependence of time and length on relative motion (or more exactly
dependence on
inertial frame of reference).
Here is not the place to go into all that, except to say that
inertial frame of reference
is an unaccelerated coordinate system.
Oh well, we can say a bit
about inertial frames.
Interactions as it turns out are not just with respect to bodies or fields.
They are also with respect to
space
or
spacetime
in
relativistic physics
But only
space
described by
inertial frames.
For example,
the ground is for many purposes---but not all---approximately an
inertial frame
To accelerate relative to the ground, a force must act on you.
But if a car accelerates relative to the ground and goes by you.
You are accelerated relative to the car, but no force causes that.
Question: Is Newton's 2nd law (F=ma) wrong?
- No.
- Yes.
- Maybe.
Answer 1 is right.
Newton's laws are defined relative to
inertial frames.
For pedagogical (or sloppiness) reasons, this is often not made clear to students.
The car does not define an
inertial frame.
The set of frames that participate in the mean expansion of the universe
are the primary
inertial frames
in modern theory.
Frames unaccelerated relative to a primary set member and local to the set
are also
inertial frames
All other local frames are not exactly
inertial frames.
Almost all physical bodies that rotate (like planets and stars) do NOT
exactly define
inertial frames.
Local Group of galaxies
Local Group
The rotation means they are accelerated relative to primay set of
inertial frames.
But like the Earth's surface such frames may be approximately inertial for
most purposes.
For some purposes one does have to correct for non-inertial frame effects.
Einstein also published
a 4th famous paper in
1905 or a 2nd one
on special relativity.
In this 4th paper he considered its further consequences
of special relativity
for mass
(Bernstein 1973, p. 97--98).
He had already shown that mass should
depend on relative motion in his first special-relativity paper.
The mass of a body measured in the
inertial frame of reference where the body is
at rest is the
rest mass.
Since mass changes with motion are minute in most human contexts
and a lot of others too, we usually just say mass for
rest mass.
But sometimes as in this section, one needs to be clear and say
rest mass
when there is any chance of ambiguity.
In the 2nd special-relativity paper or, as we will call it, the
E=mc**2 PAPER,
Einstein
deduced that all mass including that
of matter in its own frame of rest should have an
associated energy.
The formula which we call the
EINSTEIN EQUATION or the
mass-energy equivalence equation or just rattle off in
lieu of any name is
E = m*c**2
where E is the total energy of an object,
m is its mass,
and
c is the speed of light in a vacuum.
Question: What is c?
- 10 m/s.
- 344 m/s.
- 2.99792458*10**8 m/s = approximately 3*10**8 m/s.
Answer 3 is right.
The vacuum speed of light is very high and
the funny effects of
special relativity
manifest themselves only when the speed of objects
approaches c to within a factor of 10 or so.
Then they show up depends on the sensitivity of your measurement, of course.
The effects turn on gradually as speed is increased.
Answer 2 is the speed of sound in air at sea level with normal conditions
and T=20 degrees C
(Wikipedia: Speed of sound).
Answer 1 is about the maximum running speed of a human---an Olympic human
that is.
Question: At firework displays, the sight and sound of an
explosion are:
- simultaneous.
- in order sight then sound.
- in order sound then sight.
Answer 2 is right. Light is faster than sound.
You-all should remember those endless 4th of July
firework displays---John Philip Sousa, etc.
It seems as if you are watching a film with the picture and
sound not synchronized properly.
In special relativity,
the vacuum speed of light
is the ultimate physical speed.
All observers in
inertial frames,
no matter what their relative motion, measure
the speed of a light beam in a vacuum to be c.
This, of course, has weird consequences for time and length, etc.,
that we won't go into that here.
Well we can say that time, length, mass, and energy all become
dependent on the frame of reference.
The fact that time flows differently in different
frames of reference is the most
mind-blowing.
We don't notice this or other special relativity
weirdness in everyday life, because these effects only become noticeable with relative speeds near the
vacuum light speed which we don't encounter
in everyday life---except for light itself which is
a special case.
But the effects are quite measurable and
special relativity
is a well verified theory.
Actually,
E=mc**2
has two readings both of which are correct.
- The first reading is that all
energy
has an associated mass
(Lawden 1975, p. 46).
For example light
has mass since it has
energy,
but it has no
rest mass
which is why it can travel at the
vacuum speed of light.
When people say light
is massless that is just a shorthand for
for saying light
has no
rest mass.
Thermal energy has an associated mass: heat a body and its mass will
increase.
Heat flows into the
body from somewhere and its energy and mass increase.
A body in motion relative to you has kinetic energy and therefore
more mass than relative to you than if it were at rest.
These associated masses or mass changes were too small to notice before
special relativity
came along
and even now are hard to detect.
But they are detected when we have sensitive enough equipment.
Actually in this reading of
E=mc**2,
a measurement of mass
is a measurement of
energy.
One can even say that the distinction between
mass
and energy
has disappeared.
The characteristics of
mass
(resistance to acceleration and gravitational attraction)
are just
characteristics of
energy.
You can say
mass
and energy
are the same thing seen in different aspects usually.
In fact, especially when speaking in the jargon of
special relativity people sometimes stop making distinction
between
mass
and energy
and just say MASS-ENERGY.
Another point about
mass-energy equivalence is
that since all
energy
has mass
a measurement of the mass
of a system is a measurement of
the energy of
the system.
Thus all forms of
energy can
be detected by one kind of measurement in principle as
discussed in Section
Conservation of Energy.
But actually, many changes in amounts of energy that occur in
everyday life though very large in energy effects are too small
to detect changes in mass.
This is why before 1905
people thought one did have
conservation of mass
in thermal and chemical reactions.
- The second reading of E=mc**2
is what has really caught people's attention.
There is a form of energy
associated with the
rest mass.
This could be called the rest-mass energy though it seems people seldom do.
The most striking thing about rest-mass energy is how large it is
for small objects.
For example,
E = 1 kg * ( 3.00*10**8 m/s )**2
= 9*10**16 J = approximately 0.1 EJ = approximately 1/5000 of world
commercial energy consumption per year
= approximately 20 megatons of TNT (explosion energy).
See
Wikipedia: Energy units
and
Wikipedia: TNT equivalent.
Question: The first (human generated) nuclear explosion
was:
- the Trinidad test near Madison, Wisconsin in 1961.
- the Trinity test near Socorro, New Mexico in 1945.
- the Triton test near Boise, Idaho in 1932.
Answer 2 is right.
I used to live in
Socorro, New Mexico---but
not during the bomb age.
Probably the best early nuclear bomb history is
The Making of the
Atomic Bomb by
Richard Rhodes.
So in principle one could change
small amounts of
rest mass energy by
human standards into large amounts of other kinds of energy
by human standards.
However, macroscopic amounts of
rest mass
are pretty stable in the human context.
In fact, it is hard to change much
rest mass
to other energy
forms in the context of most places in the
universe including
where we live.
You could do it with the right ingredients.
Say you had a kilogram of matter and a kilogram of
antimatter.
Ramming together they would tend to annihilate and create intense electromagnetic
radiation.
Eventually, all the antimatter
would be gone (and about 1 kg of ordinary matter too)
and about 18*10**16 J of radiation and heat would be left.
But antimatter
on
Earth
and in observable universe
(so far as we can tell)
only exists in microscopic traces as a result of certain nuclear and high-energy particle
reactions.
Neither nature or we can more
than build up microscopic traces.
Antimatter keeps annihilating
with ordinary matter before it can accumulate.
Other imaginable processes for direct conversion of ordinary lumps of rest mass.
into other form of energy have their difficulties.
But on the whole this good---we don't want people or
nature setting off
megaton explosions everywhere.
Minute changes in
rest mass
happen all the time since all
energy
has associated mass.
For example, since all
energy
has mass,
chemical reactions
that release or
absorb energy change
rest mass,
but by such minute amounts that they are almost undetectable.
Before
E=mc**2
came along people took
rest mass
(then just called mass) as an absolutely conserved quantity.
The
conservation of
(rest) mass is now seen as only as an approximate result for
cases where energy changes for an object of (rest) mass m
are much less than mc**2.
It is still very useful of course.
Say a chemical reaction in a sample released 1 joule of energy from chemical bond
energy to heat energy.
If the heat all stayed in the sample, the sample mass would not change since
the heat energy just has the mass previously had by the chemical bonds.
If all the heat flowed out of the sample, the sample mass would decrease by
Delta m = E/c**2 = 1 J/(3*10**8)**2 =approximately 10**(-17) kg .
Such mass changes were unmeasurably small before 1900 and may not be
measurable even today.
I imagine chemical-reaction mass changes can be measured nowadays, but
that's just a guess.
In our environment, the biggest relative changes in
rest mass
are occur for
nuclear reactions.
Chemical reactions
change the chemical bonds of molecules.
Nuclear reactions
change the nuclear force bonds of the atomic nuclei.
There is some analogy between the two cases, but there are many differences
and one of them is the scale of the
energy
released or absorbed.
Nuclear reactions
are typically of order 10**6 (or a million) times more energetic than
chemical reactions.
That factor of 10**6 has mesmerized people ever since early days after
the discovery of
radioactivity
in 1896
which preceded the discovery of the
atomic nucleus
in 1911.
People were effectively doing
nuclear physics
before they knew they were doing that.
It is WRONG to say that
Einstein's
discovery of
E=mc**2
was the singularly important ingredient in development of
nuclear reactions
for
commercial
nuclear power
and
for
nuclear weapons.
There is a whole complex of important ingredients which are
inextricably interconnected.
But
E=mc**2
is certainly one of the ingredients as well as being
an immensely important discovery of pure science.
Almost all of modern physics is inextricably interconnected.
So it's impossible to imagine taking away a key result like
E=mc**2
without the whole edifice collapsing.
So
E=mc**2
and many other results stand or fall together.
And they do stand.
It's like a house of cards---but one that
doesn't fall down.
Actually, Einstein
rather than immediately seeing
E=mc**2
as a key to
energy
from
rest mass
saw that
the huge energy changes that happen in
radioactive decay
(then unrecognized as
nuclear reactions)
compared to
chemical reactions
meant that changes of masses could possibly be measured.
An observation of these changes would be an experimental verification of
E=mc**2.
``It is not impossible that with bodies whose energy-content is
variable to high degree (e.g., with radium salts) the theory
may be successfully put to the test.''
---Einstein's
penultimate sentence in his E=mc**2 PAPER as quoted by
Bernstein (1973, p. 98).
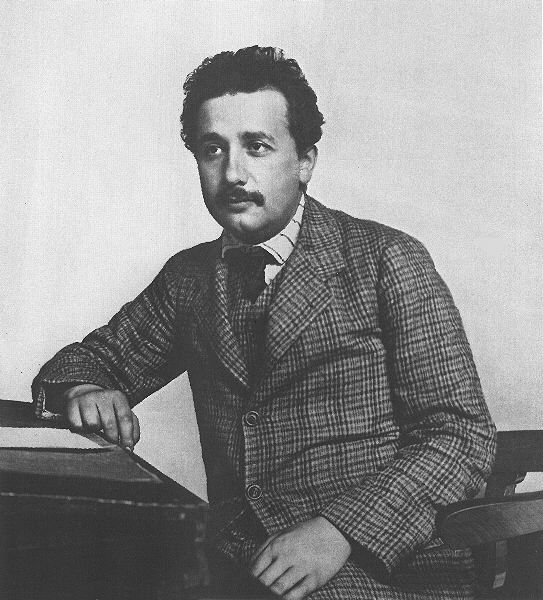Albert
Einstein (1879--1955) circa 1905.
