---



Caption: Animations illustrating dynamically the sound waves and Doppler effect (i.e., the classical Doppler effect) for an ideal isotropic point source of sound producing a continuous stream of wave cycles at a fixed frequency in its own reference frame.

The source is moving with a range of velocities (Mach 0, Mach 0.7, Mach 1.0, Mach 1.4) with respect a medium.

Features:

1. Mach number is the source velocity v in units of the sound speed v_ph (i.e., phase velocity) of the propagation medium. Thus Mach number = v/v_ph.

2. The sound waves from point source are spherical waves with respect to the medium.

   The spherical waves in the animations are seen in cross section.

   The squeezing/stretching of the wave relative to the Mach = 0 case show the degree of blueshift/redshift.

3. Our ideal source does NOT give exactly the behavior of a jet aircraft, but it mimics it for our explanatory purposes.

   Now a real jet creates series of sound waves (i.e., pressure waves) as it propagates that travel outward in all directions. The source of the sound waves are probably all kinds of vibrations associated with the jet motion and their frequencies probably do depend on jet speed.

   If the jet is sonic , or supersonic sonic the waves in some directions will merge into shock waves that are heard as sonic booms.

4. Quick description of the animations:
   1. Figure 1: Mach = 0. The source is unmoving in the medium. There is NO Doppler shift for any observer.

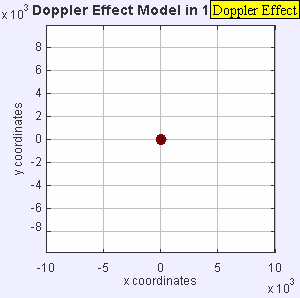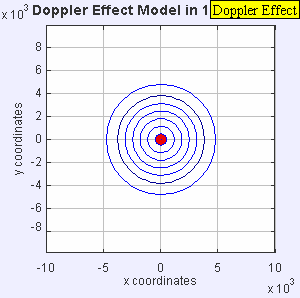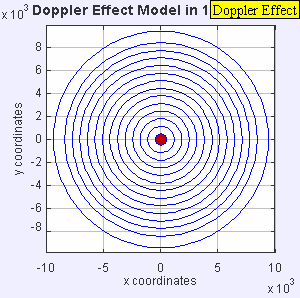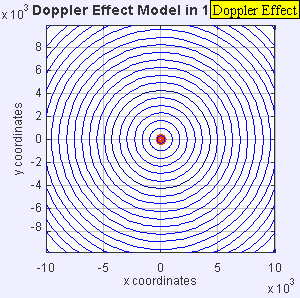
   2. Figure 2: Mach = 0.7. The source is subsonic, and so the source does NOT outrun the waves in any direction.

   3. Figure 3: Mach = 1.0. The source is sonic, and so keeps keeps up with the waves emitted in the forward direction. These forward waves pile up on each other and merge into a shock wave. The shock wave would build up to infinite amplitude if dissipation processes didn't keep turning sound energy into waste heat. The shock wave gives a sonic boom. Only observers close to path of the source (i.e., at small impact parameter) would get the full sonic boom.

   4. Figure 3: Mach = 1.4. The source is supersonic and so outruns the waves in the forward direction and leaves a trail of expanding spherical waves in its wake.

   Under reconstruction below

   The diagram illustrates physical system.

   We take the observer to be at x = 0 and a perpendicular of length h stretches from the trajectory of the moving source to the observer. The length h is called impact parameter, in fact.

5. Recall the general classical Doppler shift formula

   f_1/(1-v_1/v_ph) = f_2/(1-v_2/v_ph) ,

   where v_1 and v_2 are the line-of-sight (i.e., propagation) direction velocities (counted positive in propagation direction of the wave) and v_ph is the medium phase velocity.

   For the given physical system, let the moving source be object 1 and the observer at rest in the medium be object 2.

   The source has v_1 ≠ 0 and fixed frequency f_1 > 0. The observer has v_2 = 0 and varying frequency f_2.

   Now for the given physical system, the general formula specializes to

   f_2 = f_1/(1-v_1/v_ph) = f_1/[1-v*cos(θ)/v_ph] ,

   where v is the source velocity counted positive to the right and θ is the angle from the horizontal to the source measured positive from the line to the left of the observer.

   Note the angle θ is for the source where the waves were emitted, NOT for where the source is when the waves were received by the observer. Note also, the time between emission and reception can formally go to infinity.

   We assume without loss of generality that v ≥ 0.

For the 4 animations cases:
1. For (v/v_ph)=0 (see animation 1 above):

  f_2 = f_1 for θ∈[0°,180°]  . 

There is NO Doppler shift in this case.
2. For (v/v_ph)∈(0,1) (i.e., for a subsonic source: see animation 2 with (v/v_ph) = 0.7):

f_2 = f_1/[1-(v/v_ph)] > f_1         for θ=0°
    = f_1/[1-(v/v_ph)*cos(θ)] > f_1  for θ∈(0°,90°)
    = f_1                            for θ=90°
    = f_1/[1-(v/v_ph)*cos(θ)] < f_1  for θ∈(90°,180°)
    = f_1/[1+(v/v_ph)] < f_1         for θ=180°  . 

There is nothing remarkable about the Doppler shift in this case.
3. For (v/v_ph)=1 (i.e., for sonic source: see animation 3 with (v/v_ph) = 1)):

f_2 = ∞                              for θ=0°
    = f_1/[1-(v/v_ph)*cos(θ)] > f_1  for θ∈(0°,90°)
    = f_1                            for θ=90°
    = f_1/[1-(v/v_ph)*cos(θ)] < f_1  for θ∈(90°,180°)
    = f_1/[1+(v/v_ph)] < f_1         for θ=180°  . 

What does the f_2 = ∞ for θ = 0° mean?

All the waves arrive at the observer simultaneously no matter when they were emitted.

Of course, θ=0° means the source is at x = - ∞, unless h = 0 and the observer is right on the source's path.

If h = 0, the waves all pile right at the source at moves along. Animation 3 shows this case explicitly.

The h > 0 case is NOT shown explicitly by animation 3 and has to be imagined.

4. For (v/v_ph) > 1 (i.e., for a supersonic sonic source: see animation 4 with (v/v_ph) = 1.4)):

f_2 = f_1/[1-(v/v_ph)] < 0         for θ=0°
    = f_1/[1-(v/v_ph)*cos(θ)] < 0  for &cos*theta; > v_ph/v
    = ∞                            for for &cos*theta; = v_ph/v 
    = f_1/[1-(v/v_ph)*cos(θ)] < f_1  for  
    = f_1/[1+(v/v_ph)] < f_1         for θ=180°  . 

Note the angles θ are for the source when the waves started out, NOT for where the source is when the waves arrive at the observer.

The time between emission and reception can formally go to infinity.

Under construction

Features Continued:
6. We take time zero to be when the source is at x = 0 and let the velocity of the source be v. Without loss of generality, we assume v > 0.

   The position of the source at any time t is x = vt. Note negative/positive time gives negative/positive position x.

   The sound speed is the phase velocity v_ph of the medium.

7. The time observation t' is given by

         t' = t + sqrt(x**2+a**2)/v_ph

            = t' + sqrt[(vt)**2+a**2]/v_ph ,

   Now it is is convenient to switch to reduced quantities: τ = vt/a, τ' = vt'/a, β = v/v_ph.

   In reduced quantities, the observation time is

         τ' = τ + β*sqrt(*tau;**2+1)

   and the delay time

         Δτ = τ' - τ = β*sqrt(*tau;**2+1)

   We note that Δτ > 0 always. So the signal is always observed after it is sent---which is a darn good thing.

8. In order understand the behavior of τ', we take the derivatives of τ' and Δτ with respect to τ to get

         dτ'/dτ = 1 + βtau;/sqrt(*tau;**2+1)       and

         dΔτ/dτ = βtau;/sqrt(*tau;**2+1) .

   Note that Δτ has a single stationary point: minimum of β at τ = 0.

   This is just as it should be: for τ = 0, the source is at x = 0 and is just a distance "a" from the observer.

   The We now consider the behavior cases different β regimes.

   Behavior cases:

   1. Subsonic case with β < 1: In this case, dτ'/dτ > 0 always and τ' is strictly increasing with τ.

      The only thing to say is the observer receives a signal for all times from τ' = -&infin to τ = +∞.

   2. Supersonic case with β ≥ 1: In this case, τ' has one stationary point which is minimum
   3. Mach 0 case has the point source at rest in the medium. In this case, the spherical waves expand from a fixed point in space and there is NO Doppler shift for an observer at rest in the medium.

   4. Mach 0.7 case has the point source in subsonic motion in the medium.

      Since the motion is subsonic, the waves outrun the point source in the forward diection (i.e., its direction of motion) as well as all other directions.

      An observer at rest in the medium, observes a Doppler shift, except along a line perpendicular to the direction of motion of the point source.

      If the point source is negative/positive of the observer, the observer observes a blueshift/redshift Mach number is less than 1. When the Mach number ≥ 1, the situation is trickier. We discuss below.

   5. We can get the Doppler shift formula for an observer at rest in the medium for all cases with a little bit of analysis.

      We say there is an observer at point on the x = 0 line a general perpendicular distance "a" from the trajectory of the point source and define time zero to be when the point source is at x = 0.

      The point source has general position x = vt where v is the point source velocity which without loss of generality we take to be positive.

      If a wavefront starts out from the point source at time t', it arrives at the observer at time t given by

            t = t' + sqrt(x**2+a**2)/v_ph

               = t' + sqrt[(vt)**2+a**2]/v_ph ,

      where v_ph is phase velocity (really phase speed) of the sound wave in the medium frame.

      Taking the differential with respect to t' gives

            dt = dt' + (v/v_ph)*vt*dt'/sqrt[(vt)**2+a**2] = dt'*[1 + βz/sqrt(z**2+1)] ,

      where β = v/v_ph is Mach number and z = vt/a.

      Now frequency f = 1/p, where p is the time for a spatial wave cycle to pass a point. If we take dt' to be period for the point source wave emission, then dt is the period for the observer.

      Thus we get the Doppler shift formula

            f = f '/[1 + βz/sqrt(z**2+1)] or S = 1/[1 + βz/sqrt(z**2+1)] ,

      where f is the observer frequency, f ' is the point source frequency, and S = f '/f is a ratio we call the relative Doppler shift.

   6. We can fully explore the Doppler effect for our system using the Doppler shift formula for S:

            S = 1/[1 + βz/sqrt(z**2+1)] ,

      1. If we Taylor expand to 1st-order in small z and small βz, we get the 1st-order Doppler shift formula

               S_1st_order = 1 - βz

         which is a valid approximation to the exact Doppler shift formula when z << 1 and βz << 1. The relative relative error grows as z and βz.

         Note the motion of point source can subsonic (β < 1), sonic (β = 1) , or supersonic sonic (β > 1) as long as βz << 1.

      2. The derivative

               dS/dz = -β/{(z**2+1)**(3/2)*[1 + βz/sqrt(z**2+1)]**2} .

         The derivative is negative for all z, except at z = ±∞ where it is zero which means z = ±∞ are the only stationary points and at the infinite discontinuity that exists if 1 + βz/sqrt(z**2+1) goes to zero which it can do for β ≥ 1.

      3. Consider the case of β < 1 (i.e., the subsonic case). In this case, there is no infinite discontinuity.

         In this case, S = 1/[1-β] at z = -∞ which is the global maximum, decreases to S = 1 at z = 0, and then decreases to S = 1/[1+β} at z ∞ which is the global minimum.

         thu Thus, as stated above in different, If the observer is in front/behind this line, it observes a blueshift/redshift Mach number is less than 1.

         Under construction below

         relative

         We now see explicitly if the frequency is to the negative/positve (i.e., t and z are negative/positive), then we have the observer observes a blueshift/redshift at least when β < 1.

      4. What if β ≥ 1?

         In this case, there is a z value for which f ' goes to infinity due to the the denominator in the Doppler shift formula going to 0: i.e., z_∞

         We can solve for this z_∞:

               0 = 1 + β*z/sqrt(z**2+1)

               -1 = β*z/sqrt(z**2+1)

               -sqrt(z**2+1) = β*z

               z**2+1 = (β*z)**2 .

               Thus, z_∞ = -1/sqrt(β**2-1) ,

         where the positive root obtained in getting the last step is NOT a solution of the original equation and has been suppressed.

      5. What does infinite frequency mean?

         For ideal case, the answer might be as follows.

         Note first frequency only goes to infinity for an instant in time for the observer which means unobservable in reality and even if ideally if you desire to think of it that way. However, in a time interval around that instant a very high frequency would be observed. The better the time resolution of the observer, the higher frequency it could observe, but no real observer has infinite resolution.

         If the high frequency were beyond its time resolution, the observer MIGHT perceive an average of nothing due oscillations that cancel on average.

         I think real systems might behave as I have just described, but I'm not sure. In real systems, there are usually many complicating effects that can completely negate the predictions of infinities made by ideal cases.

      6. What about supersonic aircraft?

         I think they are significantly different from ideal system. It produces a continuous stream of wave cycles with wavelength that depends on source velocity and the direction of emission.

         Supersonic aircraft produce a single shock wave with a cone shape and a wavelength that depends on the aircraft along with ??? velocity and the direction of emission???.

         So an ordinary Doppler effect analysis doesn't apply. The wavelength CANNOT be squeezed to zero.

         What does apply is that there is time for an observer at rest when the emission from a supersonic aircraft is concentrated. This time is the conical shock wave (which is manifested as a sonic boom) passes the observer.

         Say in its own frame, the supersonic aircraft produces constant sound intensity I'. The integrated sound intensity in time Δ t' is I'Δt' assuming no canceling interference

         The observer detects the same integrated sound intensity I'Δt' in time time interval Δt.

         The observer detects sound intensity I = I'Δt'/Δt

Credit/Permission: © Loo Kang Wee (AKA User:Lookang), 2011 / Creative Commons CC BY-SA 3.0.
Local file: local link: doppler_effect_sonic.html.
Image link: Wikimedia Commons.
File: Waves file: doppler_effect_sonic.html.


---