Caption: Animations illustrating dynamically the sound waves and Doppler effect (i.e., the classical Doppler effect) for an ideal point source of sound that produces an isotropic continuous stream of wave cycles at a fixed frequency in its own reference frame.

The REFERENCE wavelength is the wavelength this source would give when it is at rest in the propagation medium for the sound waves.

In the animations, the source is moving with a range of velocities (Mach 0, Mach 0.7, Mach 1.0, Mach 1.4) with respect to the medium.

Features:

1. Mach number is the source velocity v in units of the sound speed v_ph (i.e., phase velocity) of the medium. Thus Mach number = v/v_ph.

2. The sound waves from point source are spherical waves with respect to the medium.

   The spherical waves in the animations are seen in cross section.

   The squeezing/stretching of the wavelength relative to the Mach = 0 case show the degree of Doppler effect: i.e., blueshift/redshift of the wavelength from the REFERENCE wavelength.

   When the waves are squeezed to merging you have a shock wave that is heard as a sonic boom. A sonic boom is a very strong constructive interference.

   The merging happens for transonic (speed of sound) motion by the source and supersonic motion by the source.

3. Our ideal source does NOT give exactly the behavior of a jet aircraft, but it mimics it for our explanatory purposes.

   Now a real jet creates series of sound waves (i.e., pressure waves) as it propagates that travel outward in all directions. The source of the sound waves are probably all kinds of vibrations associated with the jet motion and their frequencies probably do depend on jet speed.

4. Quick description of the animations:
   1. Figure 1: Mach = 0. The source is unmoving in the medium. There is NO Doppler shift for any observer.

   2. Figure 2: Mach = 0.7. The source is subsonic, and so the source does NOT outrun the waves in any direction.

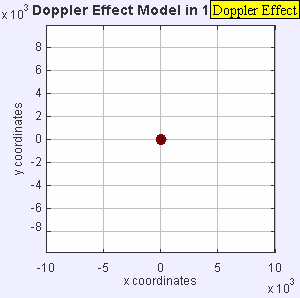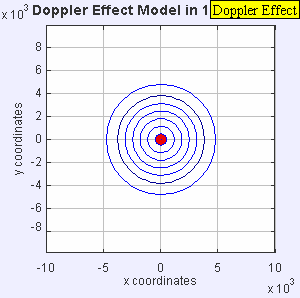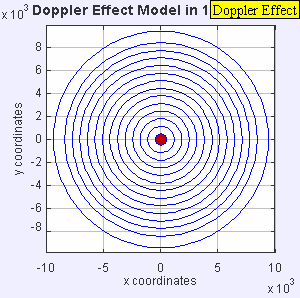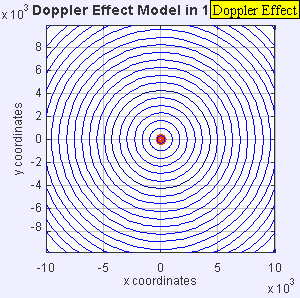
   3. Figure 3: Mach = 1.0. The source is transonic, and so keeps keeps up with the waves emitted in the forward direction. These forward waves pile up on each other and merge into a shock wave. The shock wave would build up to infinite amplitude if dissipation processes didn't keep turning sound energy into waste heat. The shock wave gives a sonic boom. Only observers close to path of the source (i.e., at small impact parameter) would get the full sonic boom.

   4. Figure 4: Mach = 1.4. The source is supersonic, and so outruns the waves in the forward direction and leaves a trail of expanding spherical waves in its wake. The spherical waves in a special direction relative to the moving source merge into a Mach cone which is the locus of a shock wave and the concomintant sonic boom.

      The Mach cone trails the moving source and is centered on its trajectory with opening angle (i.e., apex angle) θ.

5. There is a simple explanation for the Mach cone and a formula for opening angle θ. However, we will NOT gives those here.

6. The classical Doppler effect formulae are derived and somewhat explicated in Waves file: doppler_effect_classical_derivation.html.

7. See also Doppler effect videos below (local link / general link: doppler_effect_videos.html):

   EOF

Images:

1. Image link: Wikimedia Commons: File:Dopplereffectstationary.gif.
   
2. Image link: Wikimedia Commons: File:Dopplereffectsourcemovingrightatmach0.7.gif.
   
3. Image link: Wikimedia Commons: File:Dopplereffectsourcemovingrightatmach1.0.gif.
   
4. Image link: Wikimedia Commons: File:Dopplereffectsourcemovingrightatmach1.4.gif.