Caption: The shown diagrams are used in the derivation below of the Doppler effect for mechanical waves in the classical limit (AKA the nonrelativistic limit) for 1-dimensional motion in a non-dispersive medium (i.e., one in which the phase speed is independent of frequency).

We are treating an ideal special case, but it's useful for understanding the Doppler effect in general and it does apply to good accuracy in some cases (e.g., sound waves in many cases).

Note that the relativistic Doppler effect has somewhat different formulae and derivation. The relativistic Doppler effect applies to electromagnetic radiation (EMR) in vacuum which is intrinsically relativistic since EMR in vacuum travels, of course, at the vacuum light speed c = 2.99792458*10**8 m/s ≅ 3*10**8 m/s .

Derivation:

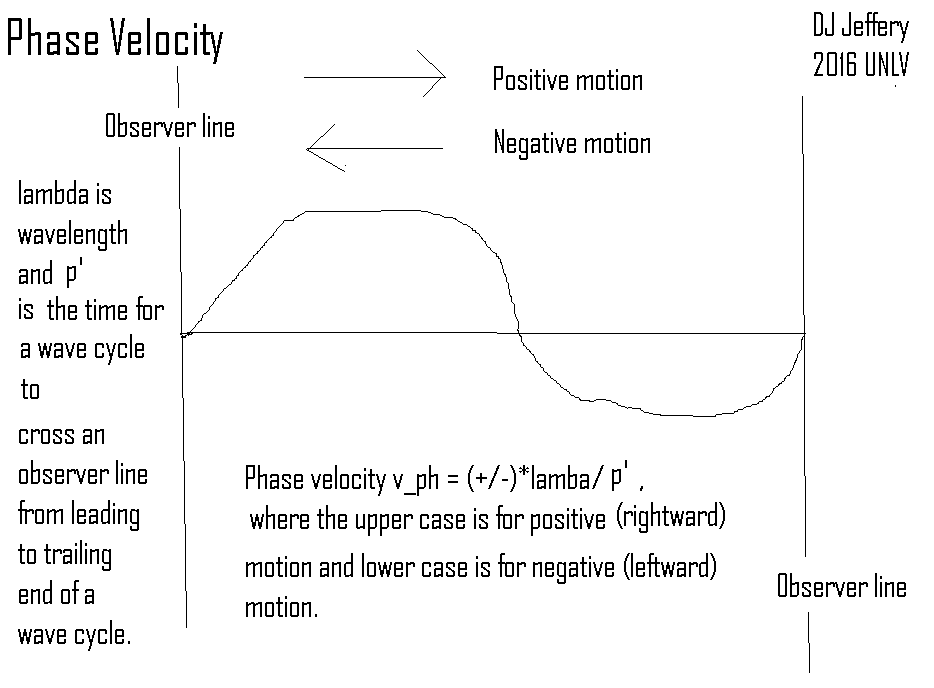
1. Phase velocity is the propagation velocity of a wave phenomenon relative to the (transmission) medium, and NOT the velocity of oscillation of whatever is oscillating to make the waves.

   The absolute value of the phase velocity (i.e., the phase speed) in the medium frame of reference is set by the nature of the waves and the (transmission) medium: it is an invariant for a given system.

   It is NOT affected by the motion of the source of the waves.

2. For our derivation, the phase velocity v_ph of waves relative to the medium reference frame is positive/negative if the waves are traveling to in positive/negative direction (i.e., to the right/left in the diagram).

   The invariant phase speed is |v_ph|.

3. The observer of the waves is moving with velocity v relative to the medium. If v > 0 / v < 0, the observer is moving in the positive/negative direction.

   Any motion of the observer perpendicular to the propagation direction gives no Doppler effect, and so we do NOT consider such motion further. We are considering just a 1-dimensional case.

4. The observer observes the waves to have observer-frame phase velocity v_ph'.

   The prime symbol means the quantity is being measured in the observer frame.

   If a quantity has NO prime, it means the quantity is explicitly a medium-frame quantity or is frame-invariant.

5. Note v_ph' = v_ph - v.

6. The wavelength λ is the length a complete spatial cycle of the waveform and is the distance between any two corresponding points on adjacent waveform cycles.

   We require the wavelength to be always positive in the formalism we develop here.

   Since our derivation is in the classical limit, length is frame-invariant, and so λ is the same for all observers no matter how they are moving. Thus, we do NOT give λ a prime for the observer frame.

   Wavelength λ DOES depend on the motion of a source as we show below.

   Also, since we are in the classical limit, the flow of time is frame-invariant too.

7. The observer-frame phase velocity must obey

         v_ph' = ±λ/p' ,

   where the upper/lower case of "±" is for waves moving in the positive/negative direction in the observer frame (NOT the medium frame) and p' is the time period it takes for a wavelength to pass the observer.

8. Clearly, N waves pass an observer in Np' periods. We define the directional frequency F ' to be the number of waves passing the observer in the positive direction to be

         F' = ± N/(Np') = ±1/p' = v_ph'/λ .

   where the positive/negative case is for the waves moving in the positive/negative direction.

   The funky directional frequency is useful in getting nice formulae without the explicit "±" symbol.

9. From the last equation follows the formula

         F'λ = v_ph'

   which is called a dispersion relation.

   It is a dispersion relation for a non-dispersive medium since directional frequency F ' and inverse of wavelength are linearly related to each other.

   The version of the dispersion relation for an observer at rest in the medium frame

         Fλ = v_ph

   where only the v_ph is, as aforesaid, the medium-frame phase velocity whose absolute value is an invariant for a given system.

   The version of dispersion relation that everyone remembers just uses absolute values:

         |F'|λ = |v_ph| ,

   where the absolute value signs are suppressed if you know what you mean.

10. Dividing the third to last formula by the second to last formula gives

          F'/F = v_ph'/v_ph = (1 - v/v_ph)

    which we rearrange to get

          F' = F(1 - v/v_ph) .

    Now we that there is a sign change between F' and F only when v/v_ph > 1 which means that the observer is, in fact, overtaking the waves: i.e., plowing into their back ends whether the waves are moving in the positive or negative direction.

    Here we introduce (ordinary) frequency f '. In the medium frame, we define f = |F| which means means the medium-frame frequency is always positive which is a darn good convention.

    Thus, have F = ±f where the upper/lower case is for positive/negative directional frequency.

    Substituting for F in the last displayed formula, we get

          F' = ±f(1 - v/v_ph)       and then       ± F' = f(1 - v/v_ph) .

    We define f ' = ±F' which when you think about it---while jumping up and down on one foot with your hands over your eyes---that f ' is only negative for v/v_ph > 1: i.e., when there is a change of sign from the always positive f: i.e., when the observer is overtaking the waves. This is a darn good result in my view.

    We now obtain

          f ' = f(1 - v/v_ph) ,

    This formula is the most basic Doppler effect formula for the classical limit.

    Many intro physics textbooks make heavy weather of the derivation of the formula, but it's really easy once you recognize that wavelength is the observer-frame invariant in the classical limit.

    Yours truly has made heavy weather of the derivation by worrying about directions of motion and the observer overtaking waves---but really you have to worry about things if you want to be general---which you do.

11. Let's explore the behavior of

          f ' = f(1 - v/v_ph) .

    Behavior:

    1. f ' > f for v/v_ph < 0 : this is a blueshift.
    2. f ' = f for v/v_ph = 0 : this is a NO Doppler shift case.
    3. 0 < f ' < f for 0 < v/v_ph < 1 : this is a redshift without the observer overtaking the waves.
    4. f ' = 0 for v/v_ph = 1 : this a redshift to zero frequency and occurs when with the observer moves at the phase velocity.
    5. -1 < f ' < 0 for 1 < v/v_ph < 2 : this is a redshift with the observer overtaking the waves.
    6. f ' = -f for v/v_ph = 2 : this is a NO Doppler shift case in my view since the absolute value of frequency has NOT changed.
    7. f ' < -f for v/v_ph > 2 : this is a blueshift in view since the absolute value of frequency has increased.

12. Now say we have a source with motion-independent fixed frequency f_source. Our conventions require |f '| = f_source in a general the source frame moving at general velocity v.

    In the medium frame, the frequency is

          f = f '/(1 - v/v_ph) ,

    f ' = |f '| = f_source if v/v_ph ≤ 1 (i.e., the source is NOT overtaking the waves it generates) and f ' = -|f '| = -f_source if v/v_ph > 1 (i.e., the source is overtaking the waves it generates). The convention for f ' for the source just ensures that medium-frame frequency f obeys the convention of always being positive.

    The wavelength of the waves is given by

          λ = |v_ph|/f = |v_ph(1 - v/v_ph)/f '| = |(v_ph - v)/f '| .

    This wavelength is, of course, frame invariant and all observers (including one moving with the source) observe it.

    Note the λ does depend on |v_ph-v| and |f '|.

    If v = 0, then λ has the value it would have for the source at rest in the medium which can be considered the source's intrinsic wavelength---but it is NOT the wavelength observed by any observer when the source is moving---that is wavelength is given by the formula above.

13. Now say the source is observer 1 with velocity v_1 and frequency f_1' and we have observer 2 who is a receiver with velocity v_2 and frequency f_2'.

    We find the general classical Doppler shift formula (hereafter just the Doppler shift formula)

          f_2' = f_1'(1 - v_2/v_ph)/(1 - v_1/v_ph) ,

    where recall v_ph gives the direction of motion of the waves by its sign.

14. Elucidating all the behavior of the Doppler shift formula is tricky, but to 1st-order exactness in small |v_1/v_ph| and | v_2/v_ph| we find the simpler 1st-order Doppler shift formula

          f_2'_1st_order = f_1'[1 - (v_2-v_1)/v_ph] ,

    where we have expanded the denominator in the geometric series and truncated to 1st-order in small |v_1/v_ph| and | v_2/v_ph|. The relative error from the exact Doppler shift formula varies as with |v_1/v_ph| and |v_2/v_ph| for |v_1/v_ph| << 1 and | v_2/v_ph| << 1.

    We see that to 1st-order the Doppler shift depends on the only the relative velocities of the source and receiver via the quantity (v_2-v_1)/v_ph NOT on the individual sizes of v_1 and v_2 as is the case for the full Doppler shift formula. In contrast, the relativistic Doppler effect in general only depends on the relative velocities.

    From the 1st-order Doppler shift formula, we see there is a redshift/blueshift when (v_2-v_1)/v_ph is positive/negative: i.e., when displacement is increasing/decreasing if we take the direction of v_ph to define the positive direction.

    Note the use of displacement, NOT distance (which is the absolute value of displacement)in the last statement. As matter of fact, redshift/blueshift when distance is increasing/decreasing too. We give the argument below when considering the Doppler shift formula.

15. The 1st-order Doppler shift formula can be written in the simplified memorable form

          Δf/f = -Δv/v_ph ,

    where Δf is change in frequency, f is either of f_1' or f_2' since it is all the same to 1st-order in small |v_1/v_ph| and | v_2/v_ph| and Δv = v_2-v_1.

    Actually, the same 1st-order formula fortuitously applies to EMR with vacuum light speed c = 2.99792458*10**8 m/s ≅ 3*10**8 m/s replacing v_ph (see Wikipedia: Relativistic Doppler effect: Motion along the line of sight).

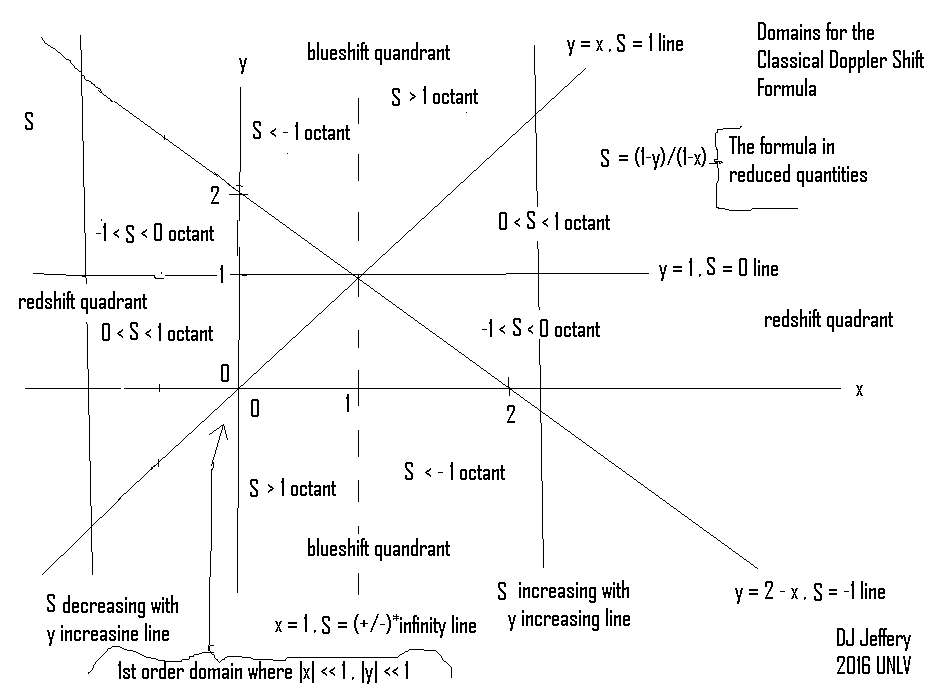
16. To elucidate all the behavior of the Doppler shift formula it is best to work in reduced quantities.

    We define the reduced quantities S = f_2'/f_1', x = v_1/v_ph, and y = v_2/v_ph and obtain the Doppler effect formula

          S = (1 - y)/(1 - x) .

    We will call S the Doppler shift and note that there is a redshift/blueshift for |S| < 1 / |S| > 1.

    Note also x and y are reduced velocities, NOT positions.

    For clarity, we will say x observer for source and y observer for receiver.

17. Using reduced velocities effectively defines the direction of wave propagation as the positive direction and makes the reduced phase velocity 1. This convention is NOT a limitation since all directions of observer motions are considered by letting x and y go negative.

    If x < 1 (i.e., the x observer reduced velocity is less than 1), there can only be waves to the right of the source since the x observer cannot outrun the waves it generates.

18. The innocent little 2-variable reduced Doppler shift formula has a rich structure.

    The diagram below illustrates its various domains of behavior in the x-y plane.

    The S would be plotted in the third dimension with an axis perpendicular to the x-y plane.

    

    To elucidate the figure:

    1. The y = x, S = 1 line gives no Doppler shift.

    2. The y = 2 - x, S = -1 line gives no Doppler shift since |S| = 1.

    3. The y = 0, S =0, has the frequency Doppler shifted to zero.

    4. The x = 0, S = ±∞ line has the frequency going to an infinite discontinuity: the exact specification is essential discontinuity. The point (x=1,y=1) is particularly the pathological. Consider the line y = s(x-1) + 1 in the x-y plane, where s is an general slope. This line always passes through point (x=1,y=1) and along the line we have S = s eveywhere except the point (x=1,y=1), where the S is undefined undefined. However, clearly the limit as you go to point (x=1,y=1) is s. This means the set of limit at point (x=1,y=1) includes all real numbers and ±∞.

    5. If you go along a vertical line with x < 1 / x > 1, S is always decreasing/increasing with increasing y. Thus these lines together with the y = x and y = 2- x lines allow us to identify which the octants have redshifts (octants with labels -1 < S < 0 and 0 < S < 1) and which have blueshifts (octants with labels S > 1 and S < -1).

    6. The 2 quadrants with |S| > 1 are the blueshift quadrants.

    7. The 2 quadrants with |S| < 1 are the redshift quadrants.

    8. Note that the 1st-order Doppler shift formula in reduced quantities is

             S_1st_order = 1 - (y-x) ,

       which is valid for |x| << 1 and |y| << 1: i.e., the small domain near the origin in the diagram.

       For the 1st-order Doppler shift formula in its domain of validity, y > x / y < x is always redshift/blueshift.

       Note since x < 1, the x observer cannot outrun the waves it generates. Thus, there are only waves to the right of the x observer.

       Thus, the y observer observes NO waves if it is left of the x observer.

       If y > x, then no matter what the initial conditions, the y observer will eventually (if not initially) be right of the x observer and observe redshifted waves. Since y < 1, the y observer cannot outrun waves once it starts seeing them, the y observer will see them as long as the setup continues.

       When the y observer is observing waves, the distance between the observers is increasing.

       If y < x, the distance between the observers is always decreasing as long as the y observer is observing waves. Once it gets left of the x observer there are no more waves to observe.

    9. Now to return to the general Doppler shift formula.

       The diagram shows that for both y > x and y < x, there are redshift and blueshift domains.

    10. Consider the y > x domain.

        Eventually (if not initially), the y observer will be right of the x observer and will observe redshifted waves only if y < 1 or either redshifted or blueshifted waves if y > 1 and x < 1 or only blueshifted waves if x >1.

        If y > 1, the y observer will eventually outrun the waves if it started a finite time in the past.

        Note that if x > 1, then the x observer will outrun the waves it generates and so the y observer (who must also obey y >1) can observe them eventually (if not initially) left of the x observer if the y observer started left of the x observer.

    11. Consider the y > x domain.

        Eventually (if not initially), the y observer will be right of the x observer and will observe redshifted waves only if y < 1 or either redshifted or blueshifted waves if y > 1 and x < 1 or only blueshifted waves if x > 1.

        If y > 1, the y observer will eventually outrun the waves if it started a finite time in the past.

        Note that if x > 1, then the x observer will outrun the waves it generates and so the y observer (who must also obey y >1) can observe them eventually (if not initially) left of the x observer if the y observer started left of the x observer.

        This means there can be an observed blueshift with the distance between the two observers decreasing.

    12. Consider the y < x domain.

        If the y observer has y > 1, then eventually (if not initially) the y observer observe redshifted waves generated by the the x observer and then will continue to observe them as long as the setup continues. If the y observer started right of the x observer, then the the distance between the observers will decrease until the x observer passes the y observer and then it will increase. So one can have a redshift with decreasing distance for awhile.

        If the y observer has y < 1 and starts left of the x observer then the y observer never observes waves.

        If the y observer has y < 1 and starts right of the x observer then the y observer will observe waves eventually (if not initially) until the x observer passes the y observer. In this case, the y observer will observe either redshifted or blueshifted waves if y < 1 and x > 1 or only blueshifted waves if x < 1.

        Note that if the y observer is right of the x observer and observes

    Credit/Permission: © David Jeffery, 2016 / Own work.
    Image links: themselves: Figure 1, Figure 2.
    File: Waves file: doppler_effect_derivation.html.
    

    ---