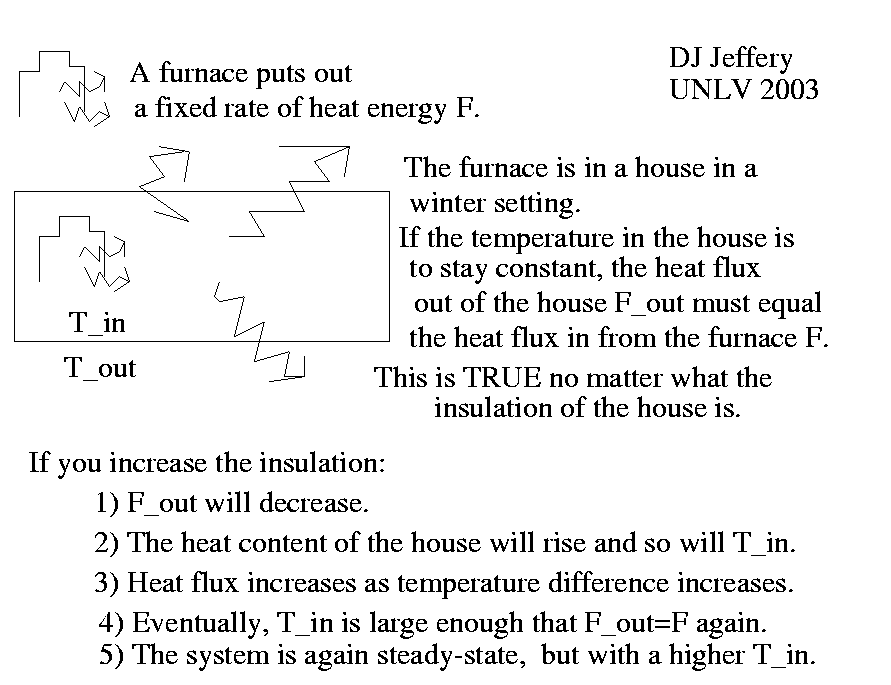
Caption: Heat flow illustrated for the steady state of a heated house with thermal insulation in cold winter conditions.

1. A Simple Analysis of the House Case (which is too simple for planets):
   1. In simple cases where the temperature gradient is NOT too steep, the heat flow depends on the temperature gradient and the amount of thermal insulation between the systems between which the heat flow is happening.

   2. The steeper the temperature gradient, the faster the heat flow.

      The more thermal insulation, the slower the heat flow.

      In simplified equation form,

        F = k(T_high - T_low) , 

      where k is thermal conductivity, T_high is the temperature of the system with the higher temperature, and T_low is the temperature of the system with the lower temperature (see Wikipedia: Thermal Conductivity: Equations).

      Note that as thermal insulation ↑, k ↓, and thus F ↓.

   3. If you have system with a fixed heat energy inflow, then system would heat up forever without an outflow.

   4. Say you have have balanced inflow F_in and outflow F_out of heat energy to a system.

      Balanced means F_in = F_out.

      The house in the image illustrates the system, where the furnace supplies F_in (which is fixed) and the outflow is to the outside.

      Inside the system the temperature is T_in and outside the temperature T_out (which is fixed).

      Since F_in = F_out, the system is in steady state and at a constant equilibrium temperature T_in.

   5. Now say you add thermal insulation to the system.

      This causes k ↓ and F_out = k(T_in - T_out) ↓.

      Now F_in > F_out and T_in ↑.

      But that makes F_out ↑.

      Eventually, F_in = F_out again and balanced is restored---but at a higher T_in than before.

   6. The upshot is that the more thermal insulation you have, the higher the equilibrium temperature.

      The A Simple Analysis of the House Case is useful in understanding the greenhouse effect, but is actually too simple.

2. Blackbody Radiator Analysis (which is still too simple for planets):
   1. The thermal-insulation system with linear dependence on temperature gradient is DIFFERENT from a pure blackbody radiator in steady state with a fixed F_in that is balanced by F_out.

      In this case, F_in fixes the temperature T uniquely as determined by the Stefan-Boltzmann law for blackbody radiation:

        F_in = F_out = σ*T**4  , 

      where we have Stefan-Boltzmann constant σ = 5.670367(13)*10**(-8) W/*m**2*K**4). Thus,

        T=sqrt(F_in/σ) 

      uniquely.

      Now if you add thermal insulation for the outflow (but NOT the inflow), you can increase T: i.e., k ↓ T ↑.

      However, the above A Simple Analysis of the House Case is too simple understand how thermal insulation quantitatively affects the Earth's surface temperature. You need to do full modeling of the Earth's atmosphere.

      But in any case, the Earth's surface temperature can be made as high as you like. If k=0, the surface temperature would increase forever.

      The Earth treated as a blackbody radiator gives a lower limit on the Earth's surface temperature. See below The Greenhouse Effect for more details on the Earth treated as a blackbody radiator.

3. The Greenhouse Effect:
   1. Now planets are actually close to being blackbody radiators, but they do have some thermal insulation provided by their planetary atmospheres (if they are NOT airless worlds) that can cause their surfaces to be hotter than otherwise.

      The situation we are considering is when the planetary atmosphere is relatively transparent to electromagnetic radiation (EMR) from the parent star inflowing to the planet surface and relatively opaque to thermal radiation (which is probably rather close to being blackbody radiation) outflowing from the surface to space. The difference transparency to inflowing and outflowing electromagnetic radiation (EMR) is due to the difference of the wavelength band of the two EMR flows.

      For example, for the Earth, the inflowing EMR is largely in the visible light band (fiducial range 0.4--0.7 μm) (to which the Earth's atmosphere is rather transparent) and the outflowing EMR is largely in the infrared band (fiducial range 0.7 μm -- 0.1 cm), (to which the Earth's atmosphere is rather opaque).

      The relative opaqueness to thermal radiation from the planet surface is the thermal insulation.

      It causes the surface temperature to rise in order to increase the emission rate of thermal radiation and establish a balance between inflow and outflow of EMR.

      This increased temperature due planetary atmosphere is the greenhouse effect.

   2. The greenhouse effect is good.

      It keeps the average surface temperature of the Earth well above the chilly surface temperature that a blackbody-radiator Earth would have.

      What the temperature of that hypothetical blackbody-radiator Earth is depends on what counterfactual assumptions you make. To see calculations of such temperatures, see Earth file: temperature_effective.html.

      But we want the right amount of greenhouse effect which is the amount the biosphere is used to having since circa 10,000 BCE (i.e., since beginning of the Holocene (∼ 11,700 BP--present) and the Neolithic (c.12,000--c.4000 BP, c.10,000--c.2000 BCE)) (see Wikipedia: Keeling curve: Mauna Loa measurements).

      At present, humankind is increasing the atmospheric carbon dioxide (CO_2) (which is the greenhouse gas after water vapor which we have NO direct control over), and so increasing the greenhouse effect and the average Earth surface temperature. For the atmospheric carbon dioxide (CO_2) trends, see NOAA: Trends in Atmospheric Carbon Dioxide. For some more details, see Wikipedia: Keeling curve: Mauna Loa measurements.

      The increasing average surface temperature could have disastrous effects for the biosphere and humankind.

   3. By the by, the greenhouse effect is a partial misnomer. It does play a secondary role in heating greenhouses---the glass windows acting as the atmosphere---but the main heating effect is that cooling upward air convection CANNOT happen in a confined building. See Wikipedia: Greenhouse effect: Real Greenhouses and Greenhouse: How Do Greenhouses Work? by Sue Ann Bowling (1941--2014).