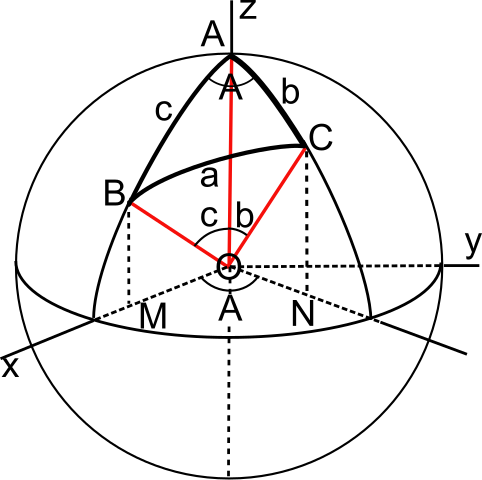
Caption: A diagram for explaining the identities of spherical trigonometry.

We will use this diagram in eplaining how to relate the angular diameter of a telescope field of view (FOV) subtended at the Earth. to the angular diameter the FOV subtends from the celestial equator at the about the same height above the celestial equator as the location of the FOV on the celestial sphere.

Explanation:

1. Note the angular diameter of a telescope FOV subtended at the Earth is also just called the FOV in a second meaning of the term FOV.

2. Some correspondances to the diagram: the celestial sphere is the sphere, the celestial axis is the z axis. the celestial equator is the equator of the sphere.

   Let R be the radius of the sphere.

3. We use radians for our angular units rather than degrees.

4. We take angle c = d and call them both θ. The declination &delta = &pi/2 - &theta is the location of an azimuthal curve curve crossing the FOV on the celestial sphere.

   The azimuthal curve has to be imagined.

   We call the the length of this curve inside the FOV be &phi.

   The angle &phi is the angular diameter the FOV subtends from the celestial equator at the about same height above the celestial equator as the location of the FOV on the celestial sphere.

5. We let the FOV angle be α. We imagine the FOV to be a cirle on the diagram sphere with its angular diameter endpoints being B and C.

6. We have two choices for the azimuthal curve: 1) its endpoints can be B and C, 2) it can pass through the center of the FOV.

7. Now for small α and &phi$, the arcs on these angles subtend on the FOV are very nearly the same and we will approximate them as being the same. Our two choices for the azimuthal curve are reduced to one choice in this approximation.

   We can now find an approximate relation between α and &phi$ that turns out to be 2nd-order good in small α and &phi$

   Let the arc length be S. Now S = α*R and S = &phi*R*&sin(θ) = &phi*R*&cos(δ).

   Solving for α gives &alpha = &phi*&sin(θ) = &phi*&cos(δ)

   For almost all practical cases, this simple relation is all you need.

8. However, we want to go further than the the simple, plus ultra even.

   Now we need spherical trigonometry which is the angle the

   UNDER CONSTRUCTION

9. A telescope FOV (for a given eyepiece) subtends a fixed angular diameter (which is also called FOV) on the sky (or celestial sphere) for the observer on Earth.

10. However, the angular diameter subtended at the celestial axis point at the vertical height of the FOV increases with with the magnitude of the height which means with the magnitude of declination of observation.

11. Now the angular velocity of the celestial sphere (360 degrees per sidereal day = sidereal hour) is for rotation about the celestial axis---it does NOT change with magnitude of declination.

12. Since the FOV

Credit/Permission: © Peter Mercator (AKA User:Peter Mercator), 2013 / CC BY-SA 3.0.
Image link: Wikimedia Commons: File:Spherical trigonometry vectors.svg.
Local file: local link: field_of_view_declination_2.html.
File: Telescope file: field_of_view_declination_2.html.