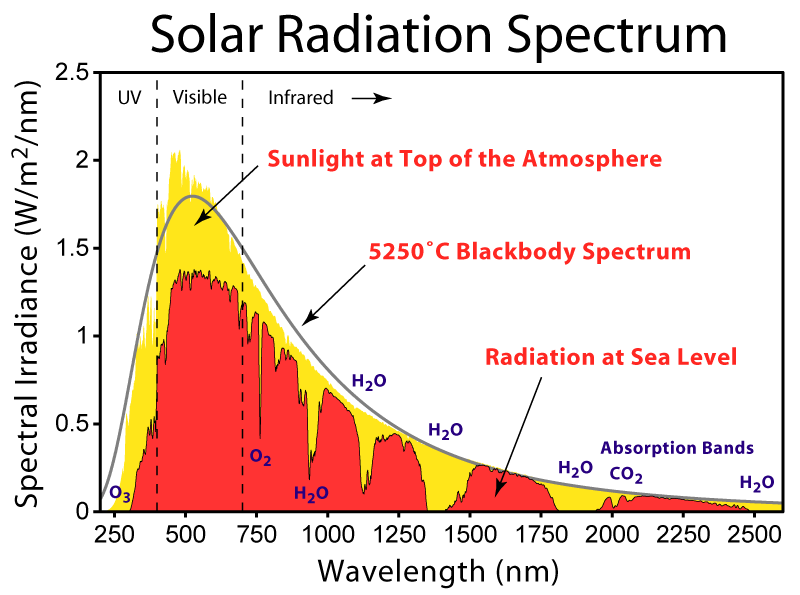
Caption: "The image shows the solar spectrum (ultraviolet band (fiducial range 0.01--0.4 μm), visible band (fiducial range 0.4--0.7 μm = 4000--7000 Å), and infrared band (fiducial range 0.7 μm -- 0.1 cm) for the range ∼ 0.2--2.5 microns (μm)) in flux (AKA intensity: more specifically spectral irradiance) for direct electromagnetic radiation (EMR) at both the top of the Earth's atmosphere and at sea level. The Sun produces EMR with a distribution similar to what would be expected from a 5523 K (5250°C) blackbody, which is approximately the Sun's surface temperature (i.e., the Sun's effective temperature). As EMR passes through the Earth's atmosphere, some is absorbed by gases with specific absorption bands (the broadest ones from molecular transitions, particularly water (see Wikipedia: Electromagnetic absorption by water) and carbon dioxide (CO_2), the main greenhouse gases, in the infrared band and ozone (O_3) in the ozone layer in the ultraviolet band). Also EMR from the blue end of the visible spectrum is preferentially Rayleigh scattered out of the paths of direct light rays from the Sun which is the Cause of the blue color of the sky." (Somewhat edited.)

Note International Astronomical Union (IAU) recommended solar effective temperature T_eff = 5772.0(8) K. The value of the solar effective temperature depends on the exact way in which it is calculated, and so varies with reference. The image value of 5523 K is probably NOT a good value in most uses.

Explication of effective temperature:

1. The effective temperature of a star, planet, or any approximately spherically symmetric object is the temperature of a blackbody radiator that has the same luminosity and radius as the object. There has to be some meaningful definition of radius for an object that has no sharply defined surface (e.g., a star).

2. The formula for effective temperature T_eff is as derived as follows:

        
     L = (4πR**2)*σT_eff**4
     
     T_eff = [L/((4πR**2)*σ)]**(1/4)  , 

   where L is the luminosity of the object and R is the radius of the object. Note F=σT**4 is the Stefan-Boltzmann law, where F is flux in units of watts (i.e., joules per second) per meter squared, the Stefan-Boltzmann constant σ = (5.67037419 ...)*10**(-8) W/*m**2/K**4 (exact) (see NIST: Fundamental Physical Constants --- Complete Listing 2018 CODATA adjustment)) and T is temperature on the Kelvin scale. For more on the Stefan-Boltzmann law, see stefan_boltzmann_law_logarithmic.html.

3. solar photosphere).